Calcule ∫ C 2 x y - 2 x d x + x 2 zd y - x 2 yd z , Onde C é a curva obtida como intersecção da superfície z = 4 - x 2 - y 2 com o plano x + y = 2 . Especifique a orientação escolhida.

Concluindo: ∫ C 2 x y - 2 x d x + x 2 zd y - x 2 yd z = 4

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 15

Calcule

Onde é a curva obtida como intersecção da superfície com o plano . Especifique a orientação escolhida.

Passo 1

Faalaa joveeem... pronto para mais uma questãozinha que envolve o Tio Stokes??

Vamos nessa!!

Como já é de lei, vamos tentar esboçar essa superfície no espaço para enxergar onde está o diaxo da intersecção.

Se tá difícil pra você tentar esboçar a superfície, tente lembrar que:

É a equação de uma esfera centrada na origem e de raio 2. Perceba então que quando ele nos diz que:

Ele quer que nós peguemos somente a metade superior desta mesma esfera, que esta no lado positivo do eixo .

Então teremos o seguinte:

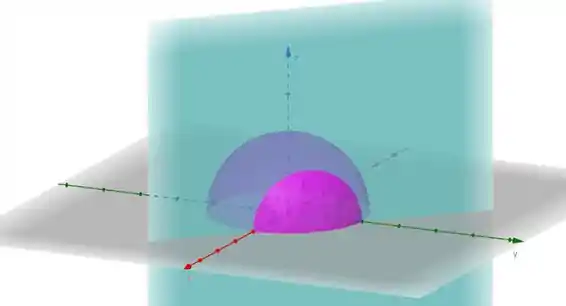
O plano é esse quadradão azul. A parte em roxo mostra mais ou menos o que seria a intersecção dos dois.

Vamos então “despoluir” essa imagem e deixar somente a superfície (S) que nos interessa:

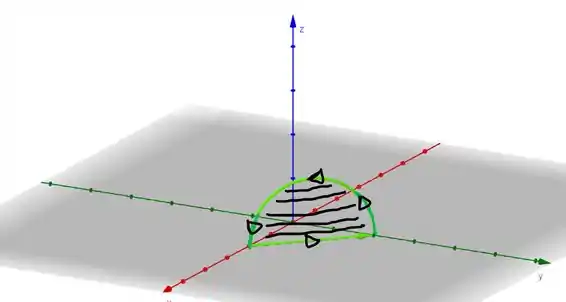
Já aproveitando a deixa para deixar definido a orientação da curva. Perceba que ela sai de um ponto e chega num ponto .

Passo 2

Bom, o que estamos fazendo mesmo?? Tentando transformar aquela integral de linha gigante em uma integral de superfície mais simples. Certo??

Ou seja:

Onde .

Beleza, então vamos obter o rotacional disso daê:

Lembra dessa formulazinha?? Se não lembrar, tente partir do determinante da matriz. Vamos chegar no seguinte resultado.

Oh God!

Mas calma! O fato da curva ser C ser fechada e o rotacional dela ser zero, só nos afirma duas coias:

Que o é um campo Gradiente; ou seja, existe uma função tal que:

O campo é conservativo; isso significa que não importa o caminho que ele percorre, somente os pontos de partida e de chegada:

Ou seja, devemos encontrar esse para então calcular a integral. O item (i) nos diz o seguinte:

Então brincando com esses termos podemos obter a função

Passo 3

Vamos lá então. Integrando em :

Encontramos:

Lembrando que aquele transmite a possibilidade de existir um termo desconhecido só em função de .

Perceba que se derivarmos em , obtemos .

Beleza, agora vamos partir do pressuposto de que aquela seja realmente a verdadeira forma da função . Se assim for, ao integrarmos ela em relação a devemos obter ; Vamos ver:

E isso aí tem que ser igual a função :

Ou seja,

O que indica que essa função é dependente somente de . Então temos um novo formato para a função :

Vamos seguir a mesma ideia e derivar isso em termos de ; esperamos obter a função :

Mas,

Portanto,

Portanto, a verdadeira forma da nossa função é a seguinte:

Com isso, podemos finalmente encontrar a integral:

Lembrando que denifimos lá no passo 1, e

Então:

Finalmente:

That’s all! See you!

Resposta

Concluindo:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. i )F → x , y , z = - y 2 i → + x 2 j → + z 2 k → ,σ é a superfície x 2 + y 2 4 + z 2 =

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. h )F → x , y , z = - y i → + x j → + x 2 k → ,σ é a superfície x 2 + y 2 + z 2 = 4 ,2 ≤

9. Calcule ∫ ∫ σ∇ × F → ⋅n →d S Onde, F x , y , z = - y , x ,e x 2 + y 2 + z 2,σ a superfície x 2+y 2+z 2=1 , z ≥ 0, e a normal apontando para fora da esfera. (Sugestão: Utilize o Exercício 8.)

8. Seja σ a superfície {(x, y, z) ∈ ℝ3 |x 2+y 2+z 2=R 2 , z ≥ 0} (R0) e seja um campo vetorial de classe C1 num aberto contendo σ. Justifique a afirmação ∫ ∫ σ∇ × F → ⋅n →d S =∫ γ F ⋅ d r Onde γ t = R

6. Seja F = ( P,Q,R ) de classe C 1 no aberto R 3 -{ ( 0,0 ,0 ) } . Seja σ a fronteira do conjunto K={ ( x ,y ,z )∈R 3|x ²+y ²-1≤z≤1-x ² -y ² } ² ² ² ² com normal apontando para fora de K. Mostre que