Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 9
9. Calcule
Onde, a superfície z ≥ 0, e a normal apontando para fora da esfera. (Sugestão: Utilize o Exercício 8.)
Passo 1
Temos assim como no exercício 8. A superfície abaixo
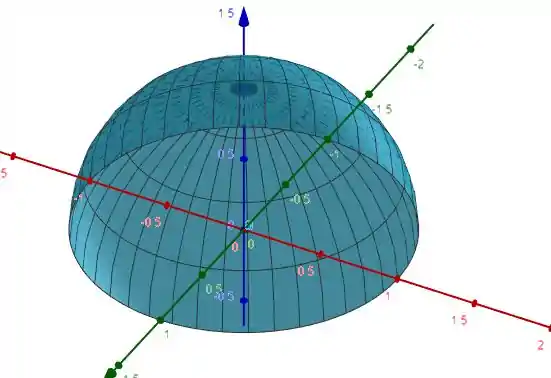
Então teremos
Ou seja, podemos parametrizar essa curva para trabalharmos apenas com uma variável. E uma possível parametrização é
Passo 2
Nossa função parametrizada fica no seguinte formato
Vamos calcular essa integral de linha
Podemos usar de propriedade trigonométrica que diz
Assim a integral fica
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 13-18, utilize a integral de superfície no teorema de Stokes para calcular o fluxo do rotacional do campo F através da superfície S na direção da normal unitária exterior n .15. F = x 2
Seja n a normal unitária exterior (normal para longe da origem) da casca parabólica S : 4 x 2 + y + z 2 = 4 , y ≥ 0 E seja F = - z + 1 2 + x i + t g - 1 y j + x + 1 4 + z k Encontre o valor ∬ ∇ × F ∙
Nos Exercícios 13-18, utilize a integral de superfície no teorema de Stokes para calcular o fluxo do rotacional do campo F através da superfície S na direção da normal unitária exterior n .13. F = 2 z
Nos Exercícios 1-6, utilize a integral de superfície no teorema de Stokes para calcular a circulação do campo F ao redor da curva C na direção indicada.6. F = x 2 y 3 i + j + z k C: A interseção do ci
Circulação ao redor de uma circunferência F = x 2 + y i + x + y j + 4 y 4 - z k C: A circunferência na qual o plano z = - y encontra a esfera x 2 + y 2 + z 2 = 4 , em sentido anti-horário quando vista