Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 8

8. Seja σ a superfície {(x, y, z) ∈ ℝ3 |   x 2   +   y 2   +   z 2   =   R 2 , z ≥ 0} (R > 0) e seja um campo vetorial de classe C1 num aberto contendo σ. Justifique a afirmação

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   ∫ γ F ⋅ d r

Onde γ t = R cos ⁡ t ,   R sin ⁡ t ,   0 ,   0 ≤ t ≤ 2π, e a normal apontandopara fora da esfera x2 + y2 + z2 ≤ R2.

Sugestao : Aplique o teorema de Stolkes às porções de supercicies regulares

σ 1   u , v =   u , v ,   R 2 - u 2 - v 2 ,   u 2 + v 2 < r 2

  0 < r < R

σ 2   ϕ ,   θ = R   s e n   ϕ cos ⁡ θ ,   R   s e n   ϕ s e n   θ ,   R cos ⁡ ϕ     ,   0 ≤ θ ≤ π  

ϕ 0 ≤ ϕ ≤ π 2

Onde ϕ 0 = arcsin ⁡ r R

σ 3 =   R   s e n   ϕ cos ⁡ θ ,   R   s e n   ϕ s e n   θ ,   R cos ⁡ ϕ   ,   π ≤ θ ≤ 2 π   ,   ϕ 0 ≤ ϕ ≤ π 2

Passo 1

Essa questão é para entender o conceito do teorema de Stokes. Que nos diz que o Fluxo vetorial através de uma superfície é igual ao Trabalho ao percorrer a borda dessa superfície. No nosso caso temos essa superfície

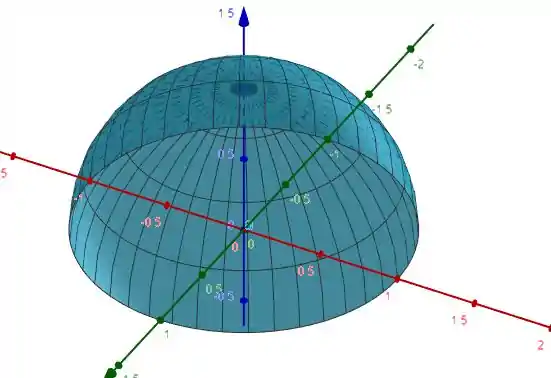
E pelo teorema podemos optar por calcular o fluxo ou o trabalho através da borda. Neste caso a borda é o circulo

x 2 + y 2 = R 2

Então teremos

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   ∫ γ F ⋅ d r = ∫ t 1 t 2 F γ t ⋅ γ ' t d t  

Ou seja, podemos parametrizar essa curva para trabalharmos apenas com uma variável. E uma possível parametrização é

γ t = R cos ⁡ t ,   R sin ⁡ t ,   0

Conseguimos provar o que o enunciado queria. Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = x 2 y 3 z i → + s e n ( x y z ) j → + x y z k → , S é a parte do cone y 2 = x 2 + z 2 que está entre os planos y = 0ey = 3
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → , S é a parte do paraboloide z = x 2 + y 2 que está dentro do cilindro x 2 + y 2 = 4
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = e - x i → + e x j → + ( e z ) k → , C é a fronteira da
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y cos ⁡ z i → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x . (Sug
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = x y z i → + x y j → + x 2 y z k → , S é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices (