Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 14

Calcule:

∫ C 4 x y - 3 x 2 z 2 d x + 2 x 2 d y - 2 x 3 z   d z

Onde C é a interseção da superfície:

x 2 3 + y 2 4 + z 2 = 1

Com z ≥ 0 , com o plano y = 1 . Indique a orientação escolhida.

Passo 1

Faaaalaa joveeem... Bora matar mais uma questãozinha.

Sem conversa, temos que esboçar os negócio lá pra poder enxergar a nossa curva.

Mas cara, que raios é aquela superfície lá?? Se a gente ignorar o z você consegue enxergar uma elipse? Quando a gente colocar o z teremos um elipsóide. Pegou a idéia?

Olha só como fica:

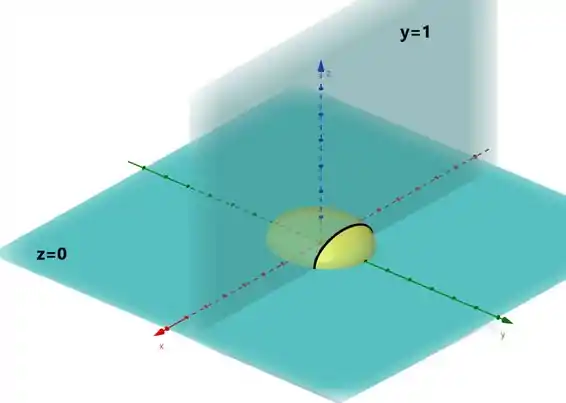
Ta mais ou menos igual aí??

Vamos despoluir esse rolê, pra enxergar melhor só aquela curva que nos interessa:

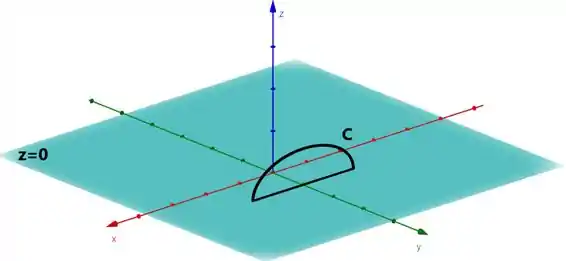
Beeelezaa, então é sob essa curva que o enunciado nos pede:

∫ C 4 x y - 3 x 2 z 2 d x + 2 x 2 d y - 2 x 3 z   d z =   ?

Maass, olha bem... vai dar um trampo né... e se a gente usar Stokes:

∮ C F   d r = ∬ S r o t F →   .     n →   d s

Pode facilitar nosso trabalho, mas aí deixamos de trabalhar sob a curva e ai vamo ter que trabalhar sob a superfície:

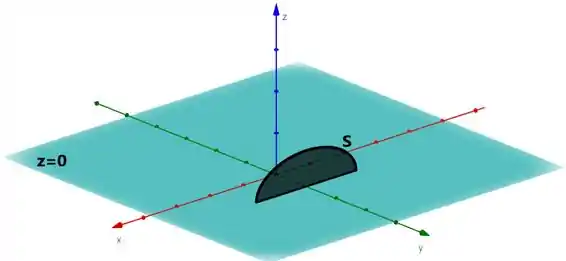
Consegue notar a diferença?? A superfície é a curva com um preenchimento ali. Só isso mesmo.

Então com isso em mente, vamos atrás do rotacional desse cara:

Passo 2

Lembra como achamos?? É assim:

r o t F → = ∇   x   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3 = ∂ F 3 ∂ y - ∂ F 2 ∂ z   ;   ∂ F 1 ∂ z - ∂ F 3 ∂ x     ;   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Onde:

F x , y , z = 4 x y - 3 x 2 z 2 ⏟ F 1   ;   2 x 2 ⏟ F 2   ;   - 2 x 3 z ⏟ F 3  

Partiu achar esses diferencial aí então:

∂ F 3 ∂ y - ∂ F 2 ∂ z = 0 - 0 = 0

∂ F 1 ∂ z - ∂ F 3 ∂ x = - 6 x 2 z - - 6 x 2 z = 0

E

∂ F 2 ∂ x - ∂ F 1 ∂ y = 4 x - 4 x = 0

Opa! Então:

r o t F → = 0   ; 0   ; 0

Isso significa que:

∮ C F   d r = ∬ S r o t F →   .     n →   d s = 0

E quando isso acontece, a gente tem duas afirmações a respeito do campo:

  1. F x , y , z é um campo gradiente, ou seja, existe uma função f x , y , z tal que:

    2. ∆ f x , y , z = F x , y , z

  2. O campo F é conservativo, ou seja:

∫ C F   d r = ∫ A B F   d r = f B - f A

Então pra obter o que o enunciado pede e gente vai precisar de um função f tal que:

∂ f x , y , z ∂ x = F 1 = 4 x y - 3 x 2 z 2             I

∂ f x , y , z ∂ y = F 2 = 2 x 2         I I

∂ f x , y , z ∂ z = F 3 = - 2 x 3 z         I I I

Uma forma de obter o que precisamos é integrando alguma dessas coisas ai em cima.

Passo 3

Vamos tentar então. Integrando I sobre x :

∫ ∂ f ( x , y , z ) = ∫ 4 x y - 3 x 2 z 2   d x

Teremos:

f x , y , z = 4 y x 2 2 - 3 z 2 x 3 3 + P y , z = 2 y x 2 - z 2 x 3 + P y , z

Lembrando sempre que temos que admitir a existência de uma função dependente somente de y e z ; mesma ideia das constantes em integrais indefinidas, lembra?

Então se admitirmos que essa é realmente a verdadeira forma dessa função f , ao derivarmos ela em relação a y , esperamos encontrar F 2 :

∂ f x , y , z ∂ y = 2 x 2 - 0 + P ' y , z

Isso tem que ser igual á:

2 x 2 - 0 + P ' y , z = 2 x 2 = F 2

A única forma de isso ser verdade é se:

P ' y , z = 0

E integrando:

P y , z = T z

Ou seja, P ou pode ser só função de z ou ser somente uma constante qualquer. Se admitirmos que ela é somente função de z , nossa f fica assim:

f x , y , z = 2 y x 2 - z 2 x 3 + T z

Se essa for a real forma de f ao derivarmos em relação a z , é de se esperar que tenhamos F 3 :

∂ f x , y , z ∂ z = 0 - 2 z x 3 + T ' z

E

0 - 2 z x 3 + T ' z = - 2 x 3 z

Isso só será verdade se T ' z = 0 e se isso acontecer, então T z = c o n s t a n t e .

Ou seja, no final da brincadeira a verdadeira forma da nossa f é:

f x , y , z = 2 y x 2 - z 2 x 3

Agora podemos jogar isso em:

∫ C F   d r = ∫ A B F   d r = f B - f A

A gente obviamente só precisa de dois pontos qualquer da curva uma vez que ele é fechada.

Então podemos optar pelos seguintes pontos:

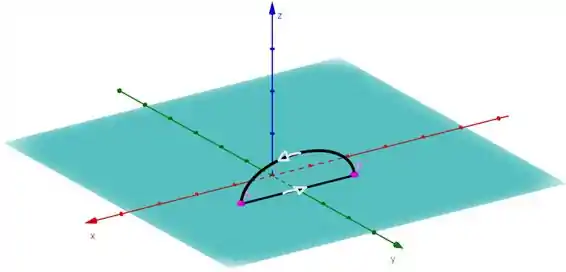
Tá, mas quais são as coordenadas desses pontos? Bom, pensa comigo y = 1 , certo? Pois é justamente o plano de interseção que nos foi dado.

E os pontos estão colados no plano x y , então z = 0 .

Podemos achar x , substituindo na fórmula do elipsóide:

x 2 3 + y 2 4 + z 2 = 1

x 2 3 + 1 4 + 0 = 1

E

x 2 3 = 3 4 → x 2 = 9 4

Ou seja:

x = ±   3 / 2

Fim de papo! Nossos pontos são:

A = 3 2   ; 1   ; 0       e       B = - 3 2 ; 1   ; 0

Substituindo esses cars na nossa f :

f A = f 3 2   ; 1   ; 0 = 2 1 3 2 2 - 0 = 9 2

E

f B = f - 3 2   ; 1   ; 0 = 2 1 - 3 2 2 - 0 = 9 2

Pois é... deu zero...

∫ A B F   d r = 9 2 - 9 2 = 0

Mas é isso!! Até a próxima!

Resposta

Concluindo:

∫ C 4 x y - 3 x 2 z 2 d x + 2 x 2 d y - 2 x 3 z   d z = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ C y + sen ⁡ x d x + z 2 + cos ⁡ y d y + x 3 d z Onde C é a curva r t = sen ⁡ t , cos ⁡ t , sen ⁡ 2 t ,0 ≤ t ≤ 2 π . (Dica: observe que C está na superfície z = 2 x y )
Use o Teorema de Stokes para calcular ∫ C F . d r . Em cada caso, C é orientada no sentido anti-horário como visto acima. F x , y , z = i + ( x + y z ) j + ( x y - z ) k C é a fronteira de parte do pl
Uma partícula se move ao longo dos segmentos de reta da origem para os pontos 1,0 , 0 , 1,2 , 1 , ( 0,2 , 1 ) e de volta a origem sob a influência do campo de força F x , y , z = z 2 i + 2 x y j + 4 y
Use o Teorema de Stokes para calcular ∫ C F . d r . Em cada caso, C é orientada no sentido anti-horário como visto acima. F x , y , z = 2 y i + ( x z ) j + ( x + y ) k C é a curva resultante da inters
Use o Teorema de Stokes para calcular ∫ C F . d r , onde F x , y , z = x 2 z i + x y 2 j + z 2 k e C é a curva resultante do plano x + y + z = 1 e o cilindro x 2 + y 2 = 9 , orientado no sentido anti-