Uma partícula se move ao longo dos segmentos de reta da origem para os pontos e de volta a origem sob a influência do campo de força
Encontre o trabalho realizado.
Passo 1
Fala, galerinha! Tudo bem?
A questão pede o trabalho realizado por uma partícula que sai e volta da origem, passando pelos segmentos de retas da origem até os pontos no campo de força:
Bom, pessoal, o trabalho feito pela força ao mover a partícula ao longo da nossa curva é dado por
O teorema de Stokes nos diz que
Onde é a fronteira da superfície orientada no sentido anti-horário. Seja a região dentro do retângulo formado pelos quatro pontos dados. Então, o que vamos precisar fazer aqui é calcular a integral:
Onde , e são componentes do rotacional de e e são derivadas parciais da nossa superfície , dada por uma equação . Então, através dos 4 pontos dados, vamos achar uma equação que descreva o plano formado por eles.
Também vamos calcular o rotacional do campo de força , assim vamos ter todos os termos da equação e é só substituir e calcularmos nossa integral dupla como já sabemos!
Bora lá!
Passo 2
Vamos começar calculando o rotacional do nosso campo de força :
Por definição, temos a seguinte equação:
Aqui, , e são as componentes do campo de força . Então:
Substituindo na equação:
Resolvendo as derivadas parciais, temos:
Pronto! Temos nosso rotacional.
Passo 3
Nós precisamos achar a equação do plano que passa pelos quatro pontos dados no enunciado, já que precisamos da equação da nossa superfície e o enunciado não deu. Aqui está o esquema dos pontos no espaço:
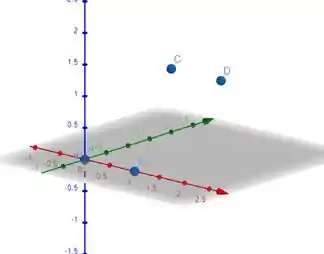
Isso é tranquilo, vamos passo a passo:
Seja a equação para um plano da forma
- No ponto do plano: (equação)
- No ponto do plano:
- No ponto do plano:
- Derivada em :
- Derivada em :
Vamos subtrair a equação da equação . Assim, temos
Substituindo o valor de na equação , encontramos que . Logo, a equação do plano se torna:
Usando a equação para substituir :
Pronto, agora temos nossa função:
Passo 4
Se a superfície é da forma e é orientada para cima, podemos usar a fórmula:
Vamos nos atentar porque aqui , e são componentes do nosso rotacional:
Retomando nosso rotacional:
Assim, temos as componentes:
Calculamos também as derivadas parciais da equação:
Agora podemos substituir na nossa equação:
Somando os termos:
Substituindo
Temos:
E subtraindo os termos da integral, ficamos finalmente com:
Passo 4
Veja que para resolvermos nossa integral dupla, ainda faltam os limites de integração da região .
é a projeção da superfície , que acaba sendo um retângulo formado no plano pelos pontos e . Se olharmos para o gráfico, podemos definir os limites de integração de e .
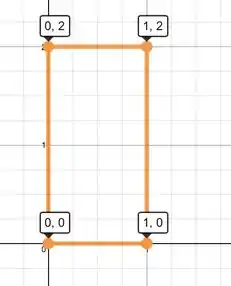
Pela imagem conseguimos ver que:
Podemos definir como . Calculando a integral, temos:
Começando a integral em , que é a integral de dentro:
Aplicando os limites de integração e integrando em :
Aplicando os limites em , temos enfim!
Então, o trabalho feito pela partícula é igual a .
Resposta
O trabalho feito é igual a .