Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2d

Calcule o volume dos sólidos W descritos abaixo.

d) É limitado pelo cone z = x 2 + y 2 , pelo cilindro x 2 + y 2 - x 2 + y 2 = x e por z = 0 .

Passo 1

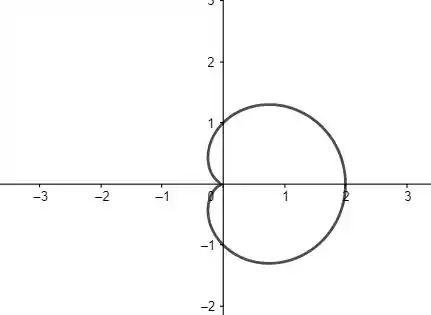
Inicialmente, note que o cilindro descrito no enunciado não é um cilindro reto normal. Ele possui a base com a forma de uma cardioide, como mostra a figura abaixo.

Passo 2

O volume da região é:

V = ∭ B d x   d y   d z

vamos determinar B . Passando para coordenadas cilíndricas, temos

x = r cos ⁡ θ y = r sin ⁡ θ z = z

Assim,

x 2 + y 2 - x 2 + y 2 = x r cos ⁡ θ 2 + r sin ⁡ θ 2 - r cos ⁡ θ 2 + r sin ⁡ θ 2 = r cos ⁡ θ r 2 - r = r cos ⁡ θ ⟹ r r - 1 = r cos ⁡ θ r - 1 = cos ⁡ θ ⟹ r = 1 + cos ⁡ θ

Sendo assim, temos que

0 ≤ r ≤ 1 + cos ⁡ θ ,   0 ≤ θ ≤ 2 π ,   0 ≤ z ≤ r ⏟ x 2 + y 2

O volume ficará:

V = ∭ B * r   d r   d θ   d z

Passo 3

Vamos calculara integral acima!

V = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ ∫ 0 r r   d z   d r   d θ V = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r   z 0 r   d r   d θ V = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r 2   d r   d θ V = ∫ 0 2 π 1 3 r 3 0 1 + cos ⁡ θ d θ V = 1 3 ∫ 0 2 π 1 + cos ⁡ θ 3   d θ V = 1 3 ∫ 0 2 π 1 + 3 cos ⁡ θ + 3 cos 2 ⁡ θ + cos 3 ⁡ θ   d θ V = 1 3 ∫ 0 2 π d θ + 3   ∫ 0 2 π cos ⁡ θ   d θ + 3   ∫ 0 2 π cos 2 ⁡ θ   d θ + ∫ 0 2 π cos 3 ⁡ θ   d θ

Calculando cada uma das integrais acima:

  1. I 1 = ∫ 0 2 π d θ = 2 π

  2. I 2 = ∫ 0 2 π cos ⁡ θ   d θ = sin ⁡ θ 0 2 π = sin ⁡ 2 π - sin ⁡ 0 = 0

  3. I 3 = ∫ 0 2 π cos 2 ⁡ θ d θ = ∫ 0 2 π cos ⁡ 2 θ + 1 2 d θ I 3 = 1 2 ∫ 0 2 π cos ⁡ 2 θ d θ + ∫ 0 2 π d θ I 3 = 1 2 1 2 sin ⁡ 2 θ 0 2 π + 2 π = 1 2 0 + 2 π = π

I 4 = ∫ 0 2 π cos 3 ⁡ θ d θ = ∫ 0 2 π cos 2 ⁡ θ cos ⁡ θ d θ I 4 = ∫ 0 2 π 1 - sin 2 ⁡ θ cos ⁡ θ d θ

Fazendo u = sin ⁡ θ ⟹ d u = cos ⁡ θ d θ . Dessa forma, segue que:

∫ 1 - sin 2 ⁡ θ cos ⁡ θ d θ = ∫ 1 - u 2   d u = u - u 3 3

Voltando para θ , temos

∫ cos 3 ⁡ θ d θ = cos ⁡ θ - 1 3 cos 3 ⁡ θ ∫ 0 2 π cos 3 ⁡ θ d θ = cos ⁡ θ - 1 3 cos 3 ⁡ θ 0 2 π = 0

Passo 4

Logo, o volume é

V = 1 3 I 1 + 3 I 2 + 3 I 3 + I 4 V = 1 3 2 π + 0 + 3 π + 0 V = 5 π 3

Observações:

  • Na integral I 2 utilizamos o fato que cos ⁡ 2 θ = 2 cos 2 ⁡ θ - 1 .
  • Na integral I 4 utilizamos a relação fundamental da trigonometria, ou seja, sin 2 ⁡ x + cos 2 ⁡ x = 1 .

Resposta

O volume vale 5 π / 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada. ∫ 0 1 ∫ 0 z ∫ 0 y z e - y 2 d xd yd z
Calcule a integral iterada. ∫ 0 π ∫ 0 x ∫ 0 x z x 2s e nyd yd zd x
Calcule a integral iterada. ∫ 0 π / 2 ∫ 0 y ∫ 0 x cos ⁡ ( x + y + z )d zd xd y
Calcule a integral tripla. ∫ ∫ ∫ E y z cos ⁡ ( x 5 )d V , onde E = x ,y ,z0 ≤ x ≤ 1,0 ≤ y ≤ x,x ≤ z ≤ 2 x }
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y