Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 5

Calcule a área do conjunto de todos os pontos θ , ρ tais que θ 2 ≤ ρ ≤ θ (coordenadas polares).

Passo 1

Antes de tudo, vamos esboçar as duas curvas no plano polar

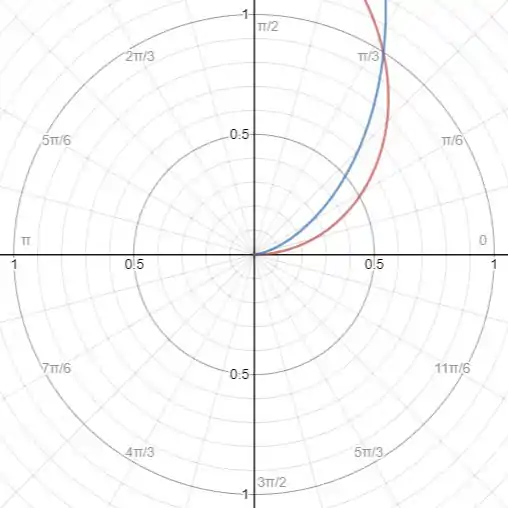
Onde a curva vermelha é referente a r = θ e a azul r = θ 2 .

Lembrando que a área de uma curva polar r e, um intervalo θ ∈ a , b é dada por

A = 1 2 ∫ a b r 2   d θ

Para calcular a área entre as duas funções pegamos a área de maior área, neste caso a vermelha, e subtraímos da de menor área, no intervalo em que elas se cruzam, ou seja

A = 1 2 ∫ θ 2   d θ - 1 2 ∫ θ 4   d θ

Neste caso elas se cruzam em θ = 0 e θ = 1 , ou seja

A = 1 2 ∫ 0 1 θ 2 - θ 4   d θ

Passo 2

Calculando as integrais

A = 1 2 θ 3 3 - θ 5 5 0 1 = 1 2 1 3 - 1 5

A = 1 2 5 - 3 15 = 1 15

Resposta

1 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a x ou a y . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região. y
Use o cálculo para encontrar a área do triângulo com os vértices dados. 0,0 ,2 ,1 ,- 1 ,6
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a x ou a y . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região. 4
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a x ou a y . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região. y
Encontre a área da região sombreada.