Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 22
Seja dada por: , e se e .
a) Esboce o gráfico de .
b) Calcule e .
c) é contínua em ? Justifique.
d) existe? E ?
c) Qual o domínio de ?
Passo 1
a) Para esboçar o gráfico, notamos o seguinte: a é quase sempre zero. A função só vai ter algum valor em cima dos eixos e (no caso, seriam parábolas).
Com estas informações básicas, o gráfico fica algo assim:
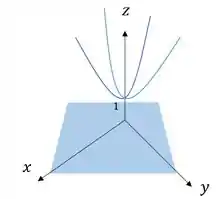
Passo 2
b) Para calcular e devemos primeiramente obter e , como a seguir:
Aplicando no ponto , obtemos
Passo 3
c) é contínua em ? Bem, se fosse verdade, não ocorreriam saltos na função e nem nas suas derivadas próximo do ponto .
Mas, pelo gráfico, percebemos que existem saltos sim! Ou seja, embora , se nos afastarmos um pouquinho em qualquer direção, digamos se pegarmos , ou qualquer valor mesmo que próximo à origem, sempre obteremos nesse valor.
Logo, não é contínua em .
Passo 4
d) existe? Vamos ser diretos: Não. Não existe! A dá um pulaço nesse ponto (em relação a ), e portanto não podemos definir a derivada em ali.
Já no ponto , a derivada está perfeitamente definida (de fato, nós já calculamos até):
Logo,
Passo 5
d) Qual o domínio de ? Bem, o domínio são todos os para os quais existe.
De fato, sabemos o seguinte:
- existe ao longo do eixo (item anterior)
- não existe ao longo do eixo (item anterior)
- existe em todos os outros pontos ( e ).
Logo, a conclusão é: o domínio de são todos os menos o eixo .
Resposta
a)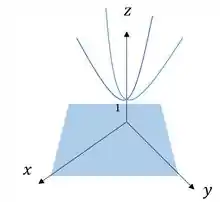 
b)
c) não é contínua em .
d) não existe. existe.
c) Todos os menos o eixo .