Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.4 - Ex. 3c

Calcule o comprimento do gráfico da função dada.

c ) f (x) = sqrt(R^2 - x^2) , - R <= x <= R , R > 0

Passo 1

Primeiro precisamos Montar a integral que descreve a área de superfície, como sabemos ela é:

int_a^b sqrt(1 + [(d (f (x)))/(d x)]^2) d x

Assim a priemira coisa a se fazer é achar a derivada da função, que é:

(d (f (x)))/(d x) = (d (sqrt(R^2 - x^2)))/(d x) = (- 2 x)/(2 sqrt(R^2 - x^2)) = - (x)/(sqrt(R^2 - x^2))

Agora substituímos:

int_(- R)^R sqrt(1 + [- (x)/(sqrt(R^2 - x^2))]^2) d x = int_(- R)^R sqrt(1 + (x^2)/(( R^2 - x^2 ))) d x = int_(- R)^R sqrt((x^2 + R^2 - x^2)/(( R^2 - x^2 ))) d x

int_(- R)^R sqrt((R^2)/(( R^2 - x^2 ))) d x = int_(- R)^R sqrt((R^2)/(( R^2 - x^2 ))) d x = int_(- R)^R (R)/(sqrt(R^2 - x^2)) d x

Depois de todo esse algebrismo vamos resolver essa integral!

Passo 2

int_(- R)^R (R)/(sqrt(R^2 - x^2)) d x

Para esse caso podemos usar substituição trigonométrica:

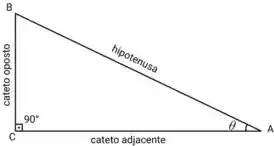
Considere o triângulo acima porém com hiopotenusa R, Cateto adjacente a theta igual a sqrt(R^2 - x^2) e cateto oposto igual a x . Com isso teremos as seguintes relações:

sec theta = (R)/(sqrt(R^2 - x^2)) e sin theta = (x)/(R) -> d x = R cos theta d theta

Fazendo as substituições necessárias:

int sec theta R cos theta d theta = int (R cos theta)/(cos theta) d theta = int R d theta = R [theta]

Lembrando que se x = R sin theta -> theta = sin^(- 1) ((x)/(R))

R [theta] = R [sin^(- 1) ((x)/(R))] (R)/(- R) = R [sin^(- 1) ((R)/(R)) - sin^(- 1) ((- R)/(R))] = R [sin^(- 1) (1) - sin^(- 1) (- 1)] =

R [(pi)/(2) - (- (pi)/(2))] = R pi

Resposta

L = int_(- R)^R (R)/(sqrt(R^2 - x^2)) d x = R pi

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área da superfície obtida pela rotação do círculo x 2 + y 2 = r 2 em torno da reta y = r .
Use o resultado do exercício 31 para escrever uma integral para encontrar a área da superfície gerada pela rotação da curva y = x ,0 ≤ x ≤ 4 , em torno da reta y = 4 . Então, use um SCA para calcular
Use um SCA para calcular a área exata da superfície obtida pela rotação da curva em torno do eixo y . Se seu SCA tiver problemas para calcular a integral, expresse a área da superfície como uma integr
Seja L o comprimento da curva y = f x , a ≤ x ≤ b , onde f é positiva e tem uma derivada contínua. Seja S f a área da superfície gerada pela rotação da curva em torno do eixo x . Se c é uma constante
Use um SCA para calcular a área exata da superfície obtida pela rotação da curva em torno do eixo y . Se seu SCA tiver problemas para calcular a integral, expresse a área da superfície como uma integr