Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 9

9 . Calcule a área da parte da superfície z = x^(3 // 2) + y^(3 // 2) , 0 <= x <= (8)/(9) e 0 <= y <= (9)/(16) x^2

Passo 1

Vamos Lembrar que nossa estrutura de cálculo é

int int_S^() d S = int int_(R ')^() sqrt(1 + ((del z)/(del y))^2 + ((del z)/(del x))^2) d y d x

E que essa região é uma seção de um paraboloide

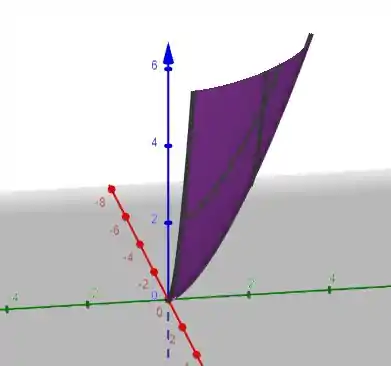
Passo 2

Então vamos usar nossa equação do paraboloide e projetar ela no plano XY

z = x^(3 // 2) + y^(3 // 2)

Logo como vamos projetar em XY, Só nos resta agora calcular as derivadas parciais de z

z_x = (3)/(2) x^((1)/(2))

z_y = (3)/(2) y^((1)/(2))

Passo 3

SHOW!!!! Vamos Unir o que já calculamos a nossa integral

int int_(R ')^() sqrt(1 + ((3)/(2) x^((1)/(2)))^2 + ((3)/(2) y^((1)/(2)))^2) d y d x

int int_(R ')^() sqrt(1 + (9)/(4) (x + y)) d y d x

Beleza Agora já temos nossa equação pra integrar. Só precisamos agora terminar descobrir o intervalo de integração. E ele será dado pelas equações de contorno do enunciado

0 <= x <= (8)/(9)

0 <= y <= (9)/(16) x^2

Vamos integrar agora

int_0^((8)/(9) ) int_0^((9)/(16) x^2) sqrt(1 + (9)/(4) (x + y)) d y d x

= (1)/(27) int_0^(8 // 9 ) (9 (x + (9 x^2)/(16)) + 4)^((3)/(2)) - (9 x + 4)^((3)/(2)) d x

= (16 (79 - 36 sqrt(3)))/(1215)

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

int int_(R ')^() sqrt(1 + ((del z)/(del y))^2 + ((del z)/(del x))^2) d y d x = (16 (79 - 36 sqrt(3)))/(1215)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∫ ∫ S x y zd S Onde S é a superfície plana 3 x + 2 y+z=12 , delimitada pelos planos y = 0 , y = 2 , x = 0 , x = 1
Calcular int int_S^() sqrt((x^2 + y^2)) d S Onde S é a superfície lateral do cone (x^2)/(4) + (y^2)/(4) - (z^2)/(9) = 0 , 0 = z = 16
Calcular ∫ ∫ S x zd S Onde S é a superfície y=x ² ², delimitada pelos planos z = 0 , z = 4 , x = 0,x = 2
Calcular ∫ ∫ S xz 2 + y 2d S Onde S é o hemisfério da frente x ²+y ²+z ²=9 ² ² ²
Calcular ∫ ∫ S x 2 + y 2d S Onde S é a superfície esférica x 2 + y 2 + z 2 = 16