Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 1-c

1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.)

  1. σ   ( u ,   v )   =   ( u ,   v ,   1   -   u   -   v ) ,   u   ≥   0 ,   v   ≥   0   e   u   +   v   ≤   1 .
  2. σ   ( u ,   v )   =   ( u ,   v ,   2   -   u   -   v ) ,   u 2   +   v 2     ≤   1 .
  3. σ   ( u ,   v )   =   ( u ,   v ,   u 2   +   v 2 ) ,   u 2   +   v 2   ≤   4 .
  4. σ   ( u ,   v )   =   ( u ,   v ,   4   -   u 2   -   v 2 ) ,   ( u ,   v )   ∈   K , onde K é o conjunto no plano uv limitado pelo eixo u e pela curva (em coordenadas polares) ρ = e - θ ,   0   ≤   θ   ≤   π
  5. σ   u ,   v =   u ,   v , 1 2 u 2 ,     0 ≤   v   ≤   u   e   u ≤ 2
  6. σ   ( u   v )   =   ( c o s   u ,   v ,   s e n   u ) ,     u 2   +   4 v 2   ≤   1  

Passo 1

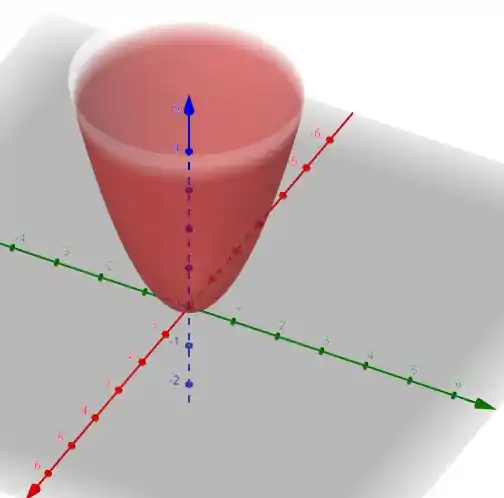
O primeiro passo é saber que superfície estamos trabalhando. A parametrização acima nos da

σ   u ,   v =   ( u ,   v ,   u 2   +   v 2 )

Sob as condições

u 2   +   v 2   ≤   4

Isso quer dizer que nossa região é um paraboloide

Passo 2

Quando quisermos calcular superfícies temos dois caminhos a seguir

∫ ∫ S d S =     ∫ ∫ R ∂ r ∂ u × ∂ r ∂ v   d u d v    

Ou

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Isso quer dizer que podemos: Parametrizar e calcular a área a partir daí. Projetar no num plano coordenado a superfície e calcular a área nessa superfície. Vou escolher a opção 2.

Passo 3

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Onde nosso z é

z =   u 2   +   v 2 )

Ou podemos escrever como

z = x 2 + y 2

Isso nos dá derivadas parciais da seguinte forma

z x =   2 x

z y =   2 y

Agora vamos jogar nossos dados na integração

∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

=   ∫ ∫ R ' 1 + 2 x 2 + 2 y 2 d y d x

Agora só precisamos encontrar os intervalos de integração. Quando Projetamos a superfície no plano XY obtermos a seguinte região em verde

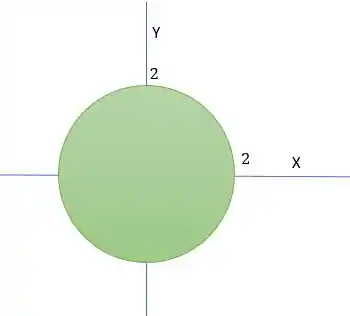
Lembra das condições iniciais u 2   +   v 2   ≤   4

Elas que nos dizem a região e assim como também os intervalos.Como estamos calculando uma região circular é melhor usarmos coordenadas polares para facilitar o cálculo. Lembrando que usamos essa regra

x 2 + y 2 = r 2

J = r

E como estamos num círculo nossos intervalos de integração são

0 < r < 2

0 < θ < 2 π

Assim nossa integral fica

∫ 0 2 π   ∫ 0 2   1 + 4 r 2   r     d r d θ

Podemos calcular por substituição sendo

u =   1 + 4 r 2

d u = 8 r   d r  

Como nossa integral não depende de θ   logo podemos integral logo por ele e substituir r  

2 π ∫ 1 8 u d u

= π 4   2 3 u 3 2

= π 6   u 3 / 2    

Agora voltamos com nossa função original e com os intervalos de integração

π 6   1 + 4 r 2 3 / 2 r = 0 2

= π 6   17 3 / 2   - 1

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ S d S =     π 6   17 3 / 2   - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a área da superfície do paraboloide z = x 2 + y 2 exterior ao cone z = x 2 + y 2
Calcular a área total da superfície cuja lateral é parte do cilindro x 2 + y 2 = 4 ; cuja parte superior é uma porção do hemisfério z = 16 - x 2 - y 2 e cuja parte inferior é a porção do plano z = 0 .
Dada a equação vetorial r → u , v = ( u cos ⁡ v ,us e nv ,u 2 ) Eliminar os parâmetros u e v determinando a equação cartesiana da superfície
Uma superfície S é representada pela equação vetorial r → u , v = cos ⁡ vi → + s e nvj → + uk → ,0 ≤ u ≤ 4 ,≤ v ≤ 2 π . Mostrar que S é uma parte de uma superfície de revolução.
Uma superfície S é representada pela equação vetorial r → u , v = cos ⁡ vi → + s e nvj → + uk → ,0 ≤ u ≤ 4 ,≤ v ≤ 2 π . Determinar a área de S