Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 4
4 . Calcule a área da parte da superfície cilíndrica que seencontra dentro do cilindro e acima do plano xy
Passo 1
O enunciado pode parecer confuso , então vamos primeiro ver com qual superfície estamos lidando.
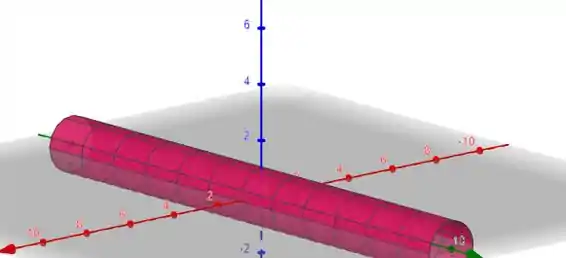
É com a parte superior desse cilindro, recortado pela região
Acho que já deu uma melhorada. Vamos escrever a estrutura do nosso calculo
Ou
Vamos usar a segunda parte.
Passo 2
Da equação do nosso cilindro
Podemos escrever
Assim as derivas parciais serão
Passo 3
Vamos plotar os dados no calculo
Agora precisamos ver quais são nosso limites de integração da aeuqação abaixo
Podemos dizer que
Logo nossa integração fica
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Calcule ∬ K f x , y , z d S sendo: d )f x , y , z = y ;σ u , v = u , v , 1 - u 2 ,0 ≤ u ≤ 1 ; 0 ≤ v ≤ u .
Calcule ∬ K f x , y , z d S sendo: d )f x , y , z = x 2 + y 2 ;σ a superfície x 2 + y 2 + z 2 = 4 ,z ≥ 1 . (Fica entendido aqui que σ é a parametrização mais “natural” do conjunto dado).
Calcule ∬ K f x , y , z d S sendo: g )f x , y , z = x ;σ é a parte da superfície z 2 = x 2 + y 2 situada entre os planos z = 1ez = 3 .
Calcule a massa da superfície σ dada, com função densidade superficial de massa f ( x , y , z ) dada: c )f x , y , z = 2 e σ u , v = u , v ,1 - u 2 ,0 ≤ u ≤ 1 ,0 ≤ v ≤ 1 .
Calcule ∬ K f x , y , z d S sendo: f )f x , y , z = x y ;σ é a interseção do paraboloide z = x 2 + y 2 com o conjunto x 2 + y 2 ≤ 2 x ,y ≥ 0 .