Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 1-d

1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.)

  1. σ   ( u ,   v )   =   ( u ,   v ,   1   -   u   -   v ) ,   u   ≥   0 ,   v   ≥   0   e   u   +   v   ≤   1 .
  2. σ   ( u ,   v )   =   ( u ,   v ,   2   -   u   -   v ) ,   u 2   +   v 2     ≤   1 .
  3. σ   ( u ,   v )   =   ( u ,   v ,   u 2   +   v 2 ) ,   u 2   +   v 2   ≤   4 .
  4. σ   ( u ,   v )   =   ( u ,   v ,   4   -   u 2   -   v 2 ) ,   ( u ,   v )   ∈   K , onde K é o conjunto no plano uv limitado pelo eixo u e pela curva (em coordenadas polares)

    5. ρ   =   e - θ     0   ≤   θ   ≤   π

  5. σ   u ,   v =   u ,   v , 1 2 u 2 ,     0 ≤   v   ≤   u   e   u ≤ 2
  6. σ   ( u   v )   =   ( c o s   u ,   v ,   s e n   u ) ,     u 2   +   4 v 2   ≤   1  

Passo 1

O primeiro passo é saber que superfície estamos trabalhando. A parametrização acima nos da

σ   u ,   v =   ( u ,   v ,   4   -   u 2   -   v 2 )

Sob as condições

ρ   =   e - θ     0   ≤   θ   ≤   π

Isso quer dizer que nossa região é um paraboloide

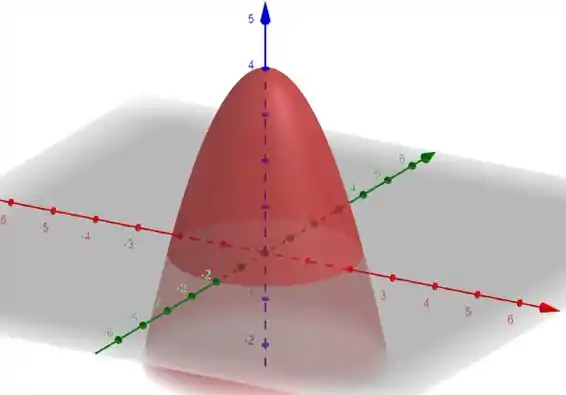
Passo 2

Quando quisermos calcular superfícies temos dois caminhos a seguir

∫ ∫ S d S =     ∫ ∫ R ∂ r ∂ u × ∂ r ∂ v   d u d v    

Ou

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Isso quer dizer que podemos: Parametrizar e calcular a área a partir daí. Projetar no num plano coordenado a superfície e calcular a área nessa superfície. Vou escolher a opção 2.

Passo 3

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Onde nosso z é

z =   4 - u 2 -   v 2

Isso nos dá derivadas parciais da seguinte forma

z u =   - 2 u

z v =   - 2 v

Agora vamos jogar nossos dados na integração

∫ ∫ R ' 1 + ∂ z ∂ u 2 + ∂ z ∂ v 2 d u d v

=   ∫ ∫ R ' 1 + - 2 u 2 + - 2 v 2 d u d v

Agora só precisamos encontrar os intervalos de integração. Quando Projetamos a superfície no plano XY obtermos a seguinte região em verde

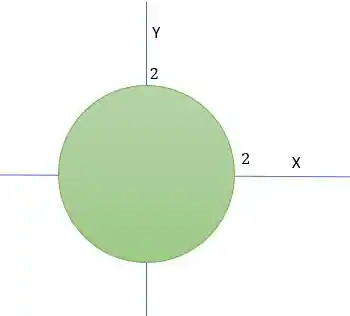
Lembra das condições iniciais ρ   =   e - θ     0   ≤   θ   ≤   π

Elas que nos dizem a região e assim como também os intervalos.Como estamos calculando uma região circular é melhor usarmos coordenadas polares para facilitar o cálculo. Lembrando que usamos essa regra

u 2 + v 2 = r 2

J = r

Assim nossos intervalos de integração são

0 < r < e - θ

0 < θ < π

Assim nossa integral fica

∫ 0 π   ∫ 0 e - θ   1 + 4 r 2   r     d r d θ

Podemos calcular por substituição sendo

u =   1 + 4 r 2

d u = 8 r   d r  

∫ 0 π   ∫ 0 e - θ   1 + 4 r 2   r     d r d θ

∫ 0 π   ∫ 0 e - θ   1 + 4 r 2   r     d r d θ = 1 12 ∫ 0 π   1 + 4 r 2 3 / 2 r = 0 e - θ     d θ  

= 1 12   ∫ 0 π 1 + 4 e - 2 θ 3 / 2 - 1     d θ

Essa integral fica enorme, porque será necessários várias substituições para resolve-la . temos portanto o resultado aproximado de 4

= 1 12 4

= 1 3    

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ S d S =     1 3    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∫ ∫ S x + y + zd S S é a face superior do cubo 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ 1 S é a face da frente do cubo do item a)
Calcular ∫ ∫ S x + y + zd S S é a face superior do cubo 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ 1 S é a face da frente do cubo do item a)
Calcular ∫ ∫ S x 2 zd S Onde S é a superfície cilíndrica x 2 + y 2 = 1; 0 ≤ z ≤ 1
Calcular ∫ ∫ S x + z d S Onde S é a superfície plana 2 x+ 2 y+z=6 , no 1º octante
Calcular ∫ ∫ S 2 zd S Onde S é a parte do paraboloide z=x ²+ y ² -2 ² ² abaixo do plano xy