Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 3a

Calcule a área da região limitada pela curva dada(coordenadas polares).

a )   ρ = 2 - cos ⁡ θ

Passo 1

A fórmula para se calcular a área da região delimitada pela cruva é:

Á r e a = 1 2 ∫ α β ρ 2 d θ

Assim, substituímos os valores que temos, sendo os limites de integração o suficiente para formar a figura.

Ela será essa área:

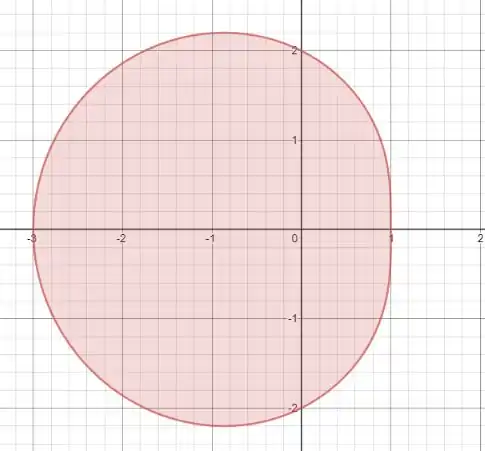
Como é simétrico em relação ao semieixo Ox, vamos usar apenas o intervalo 0 ,   π e multiplicamos por 2, vai ficar:

Á r e a = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ 0 2 π 2 - cos ⁡ θ 2 d θ = ∫ 0 π 2 - cos ⁡ θ 2 d θ

Passo 2

Á r e a = ∫ 0 π 2 - cos ⁡ θ 2 d θ = ∫ 0 π 4 - 4 cos ⁡ θ + cos 2 ⁡ θ d θ =

∫ 0 π 4 d θ - ∫ 0 π 4 cos ⁡ θ d θ + ∫ 0 π cos 2 ⁡ θ =

4 × π - 4 sin ⁡ θ π 0 + ∫ 0 π 1 2 1 + cos ⁡ 2 θ d θ = 4 π + 1 2 θ + sin ⁡ 2 θ 2 π 0 =

4 π + 1 2 π = 8 π + π 2 = 9 π 2

Resposta

Á r e a = 9 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7-18 Esboce a região englobada pelas curvas e encontra a área16. y = 1 1 - x 2 , y = 2
7-18 Esboce a região englobada pelas curvas e encontra a área18. y = x , y = 4 x , y = - x + 2
Encontre a área da região sombreada:
Encontre a área da região sombreada integrando em relação a x:
Encontre a área da região sombreada: