Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 4d

Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares

d )   ρ 2 = cos ⁡ θ   e   ρ 2 = sin ⁡ θ   ( ρ ≥ 0 )

Passo 1

Primeiro devemos achar os pontos de intersecção das funções:

sin ⁡ θ = cos ⁡ θ → tan ⁡ θ = 1

Nesse caso vemos que dentro do intervalo 0 ,   2 π teremos só um valor ideal para esse θ que vai ser π 4   , mas pela imagem o sin ⁡ 0 = cos ⁡ π 2 , a imagem ficou assim:

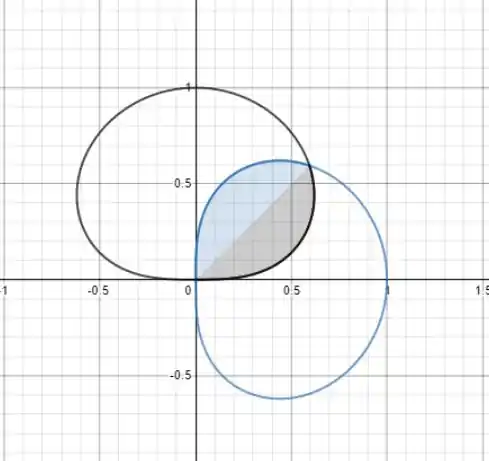
Na imagem vemos que a intersecção acontece em θ = π 4 , mas também ocorre para c o s θ quando θ = π 2 e sin ⁡ θ   quando θ = 0 , então vamos considerar o intervalo para a área do cos ⁡ θ no inervalo π 4 , π 2 e para sin ⁡ θ no intervalo 0 , π 4 .

Passo 2

Daí calculamos cada área:

Á r e a   1 = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ 0 π 4 sin ⁡ θ 2 d θ = 1 2 ∫ 0 π 4 sin ⁡ θ d θ

E

Á r e a   2 = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ π 4 π 2 cos ⁡ θ 2 d θ = 1 2 ∫ π 4 π 2 cos ⁡ θ d θ

Agora vamos calcular cada área e depois somamos:

Á r e a   1 = 1 2 ∫ 0 π 4 sin ⁡ θ d θ = - 1 2 cos ⁡ θ π 4 0 = - 1 2 2 2 - 1 = 1 2 - 2 4

Á r e a   2 = 1 2 ∫ π 4 π 2 cos ⁡ θ d θ = 1 2 sin ⁡ θ π 2 π 4 = 1 2 1 - 2 2 = 1 2 - 2 4

Passo 3

Agora somamos:

1 2 - 2 4 + 1 2 - 2 4 = 1 - 2 2

Resposta

Á r e a = 1 2 ∫ 0 π 4 sin ⁡ θ d θ + 1 2 ∫ π 4 π 2 cos ⁡ θ d θ = 1 - 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região sombreada:
Encontre a área da região sombreada:
Encontre a área da região sombreada integrando em relação a y:
Encontre a área da região sombreada integrando em relação a y:
Encontre a área da região sombreada integrando em relação a x: