Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 3d

Calcule a área da região limitada pela curva dada(coordenadas polares).

c )     ρ = cos ⁡ 3 θ

Passo 1

A fórmula para se calcular a área da região delimitada pela cruva é:

Á r e a = 1 2 ∫ α β ρ 2 d θ

Assim, substituímos os valores que temos, sendo os limites de integração o suficiente para formar a figura.

Ela será essa área:

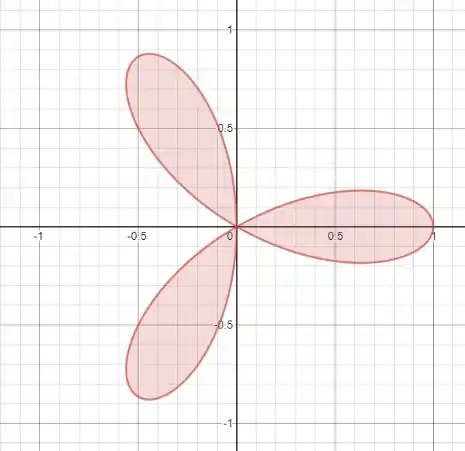
Vemos 3 pétalas com áreas iguais o intervalo para criar uma pétala são os valores que se jogarmos na equação teremos 0, ou seja, os dois primeiros zeros da nossa tabela.

Se fosse uma equação ρ = cos ⁡ θ o intervalo seria: - π 2 , π 2 , mas como temos a equação:

  ρ = cos ⁡ 3 θ , vamos pegar ânguos com módulo 3 vezes menor, ou seja - π 6 , π 6 .

Ok! Agora temos uma pétala, como são 3 multiplicamos a equação por 3:

Á r e a = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ 0 2 π cos 2 ⁡ 3 θ d θ = 3 2 ∫ - π 6 π 6 cos 2 ⁡ 3 θ d θ

Passo 2

Á r e a = 3 2 ∫ - π 6 π 6 cos 2 ⁡ 3 θ d θ =

Temos que usar aqui a relação: cos 2 ⁡ θ = 1 2 1 + cos ⁡ 2 θ , porém nosso θ =   3 θ → cos 2 ⁡ 3 θ = 1 2 1 + cos ⁡ 6 θ

3 2 ∫ - π 6 π 6 1 2 1 + cos ⁡ 6 θ d θ = 3 4 ∫ - π 6 π 6 1 + cos ⁡ 6 θ d θ

Fazemos a substituição: u = 6 θ → d u = 6 d θ

3 24 ∫ - π π 1 + cos ⁡ u d u = 1 8 ∫ - π π 1 + cos ⁡ u d u

θ 8 + ( sin ⁡ u ) 8 π - π = π 8 + ( sin ⁡ π ) 8 - - π 8 + ( sin ⁡ ( - π ) ) 8 = π 8 - - π 8 = 2 π 8 = π 4

Resposta

Á r e a = π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da superfície obtida quando a curva y = 25 - x 9≤x≤16 gira em torno do eixo x .
(a) Apresente uma soma de integrais definidas que represente a área total entre as curvas y = f ( x ) e y = g ( x ) na figura abaixo.(b) Encontre a área total delimitada por y = x 3 e y = x no interva
Seja C a curva 27 x - y 3 = 0 entre y =0 e y=2 . Em cada parte, monte, mas não calcule, uma integral ou somas de integrais que resolvam o problema.(a) Encontre a área da superfície gerada quando C gir
A figura abaixo mostra as curvas velocidade versus tempo para dois carros movendo-se ao longo de uma pista reta, começando no mesmo ponto e acelerando a partir do repouso.(a) Qual é a distância entre
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. y = x e x 2 , y = 2 | x |