Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 4d

Calcule a área das seguintes superfícies.

d) Superfície da esfera x 2 + y 2 + z 2 = 12 que não está no interior do paraboloide z = x 2 + y 2 .

Passo 1

Veja o esquema abaixo:

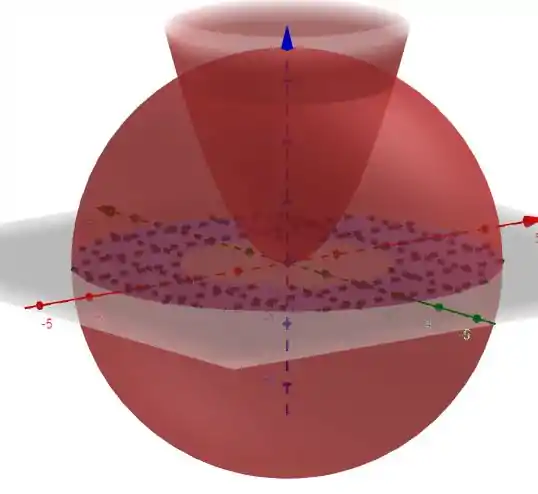
A área que desejamos é toda a área da esfera menos a que se encontra no interior do paraboloide. Sejam:

  • A a área desejada;
  • A 1 a área total da esfera;
  • A 2 a área da esfera no interior do paraboloide.

Veja que

A = A 1 - A 2

Passo 2

Vamos começar calculando A 1 . Note que a esfera possui raio R = 12 . Sendo assim,

A 1 = 4 π R 2 A 1 = 4 π 12 2 A 1 = 48 π

Passo 3

Para calcular A 2 vamos tomar a parametrização:

φ x , y = x ,   y ,   12 - x 2 - y 2

Vamos determinar a região em que x , y estão limitados.

x 2 + y 2 + z 2 = 12 z = x 2 + y 2

Assim, colocando a 2° equação na 1°, temos:

z + z 2 = 12 z 2 + z - 12 = 0 z - 3 z + 4 + 0

Logo, z = 3 ou z = - 4 . Note que esse último valor não faz sentido, pois se z = x 2 + y 2 , então z pode assumir apenas valores positivos ou nulo. Assim:

z = 3

Colocando isso na segunda equação,

x 2 + y 2 = 3

Ou seja, x , y estão no interior de uma circunferência de raio 3 .

Passo 4

A área A 2 pode ser calculada por:

A 2 = ∬ D ∂ φ ∂ x × ∂ φ ∂ y   d x   d y

Note que já calculamos esse produto vetorial no item c). Usando o resultado obtido lá, temos:

∂ φ ∂ x × ∂ φ ∂ y = 12 12 - x 2 - y 2

De maneira que

A 2 = ∬ D 12 12 - x 2 - y 2   d x   d y

Aqui, uma boa saída é usarmos coordenadas polares. Façamos

x = ρ cos ⁡ θ y = ρ sin ⁡ θ

de maneira que x 2 + y 2 = ρ 2 . Lembrando que x , y estão no interior do círculo de raio 3 , então:

0 ≤ x 2 + y 2 ≤ 3 0 ≤ ρ 2 ≤ 3 0 ≤ ρ ≤ 3

Sendo assim,

A 2 = ∫ 0 2 π ∫ 0 3 12 ρ 12 - ρ 2 d ρ   d θ A 2 = 2 π 12   ∫ 0 3 ρ 12 - ρ 2 d ρ

Para calcular essa última integral, façamos u = 12 - ρ 2 . Logo,

d u = - 2 ρ   d ρ ∴ ρ   d ρ = - d u / 2 ρ = 0 ⟹ u = 12 ρ = 3 ⟹ u = 9

Portanto,

A 2 = 2 π 12 ∫ 12 9 u - 1 2   - d u 2 A 2 = π 12   ∫ 9 12 u - 1 2   d u A 2 = π 12 u 1 / 2 1 / 2 9 12 A 2 = 2 π 12 12 - 3 A 2 = π 24 - 6 12

Passo 5

Finalmente, temos que

A = 48 π - 24 - 6 12 π A = 24 + 6 12 π A = 6 4 + 12 π

Resposta

A área vale A = 6 4 + 12 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6 . Calcule a área da superfície z = x 2 + y ²,x - 2 2 + 4 y 2 ≤ 1 ²
12 . Calcule a área da parte da superfície z=x y que se encontra dentro docilindro x 2+y 2≤4 e fora do cilindro x 2+y 2≤1
2 . Seja A=0 ,y ,z ∈R 3z 2+y-2 2=1 } ; ache a área da superfíciegerada pela rotação em torno do eixo Oz do conjunto A.
7 . Calcule a área da superfície esférica x 2+y 2+z 2=2 que seencontra dentro do paraboloide z=x 2+y 2
4 . Calcule a área da parte da superfície cilíndrica z 2+x 2=4 que seencontra dentro do cilindro x 2+y 2≤4 e acima do plano xy