Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 4g

Calcule a área das seguintes superfícies

g) Superfície da esfera de raio a centrada na origem limitada por dois planos paralelos e dois meridianos, sabendo-se que o ângulo entre os meridianos é α e a distância entre os planos que contém os paralelos é h .

Passo 1

Para facilitar, vamos tomar um plano como sendo o plano x y . O outro plano será z = h . Tomando um dos meridianos como sendo o plano x z .

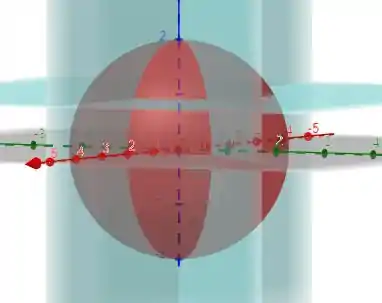
Uma boa parametrização é tomarmos:

φ θ ,   ϕ = a cos ⁡ θ sin ⁡ ϕ ,   a sin ⁡ θ sin ⁡ ϕ ,   a cos ⁡ ϕ

Notemos que:

arccos ⁡ h a ≤ φ ≤ π 2 0 ≤ θ ≤ α

Passo 2

Dessa maneira, segue que

A = ∬ D ∂ φ ∂ θ × ∂ φ ∂ ϕ   d θ   d ϕ

onde

D = θ ,   ϕ ∈ R 2 : arccos ⁡ h a ≤ φ ≤ π 2 ,   0 ≤ θ ≤ α

Vamos então calcular as derivadas.

Passo 3

  • Cálculo de ∂ φ / ∂ θ :

    • ∂ φ ∂ θ = ∂ ∂ θ a cos ⁡ θ sin ⁡ φ , ∂ ∂ θ a sin ⁡ θ sin ⁡ φ , ∂ ∂ θ a cos ⁡ φ ∂ φ ∂ θ = - a sin ⁡ θ sin ⁡ φ ,   a cos ⁡ θ sin ⁡ φ ,   0

  • Cálculo de ∂ φ / ∂ ϕ :

∂ φ ∂ ϕ = ∂ ∂ ϕ a cos ⁡ θ sin ⁡ ϕ , ∂ ∂ ϕ a sin ⁡ θ sin ⁡ ϕ , ∂ ∂ ϕ a cos ⁡ ϕ ∂ φ ∂ ϕ = a cos ⁡ θ cos ⁡ ϕ ,   a sin ⁡ θ cos ⁡ ϕ ,   - a sin ⁡ ϕ

Logo,

∂ φ ∂ θ × ∂ φ ∂ ϕ = i j k - a sin ⁡ θ sin ⁡ ϕ a cos ⁡ θ sin ⁡ ϕ 0 a cos ⁡ θ cos ⁡ ϕ a sin ⁡ θ cos ⁡ ϕ - a sin ⁡ ϕ ∂ φ ∂ θ × ∂ φ ∂ ϕ = - a 2 cos ⁡ θ sin 2 ⁡ ϕ ,   - a sin ⁡ θ sin 2 ⁡ ϕ ,   - a 2 sin 2 ⁡ θ sin ⁡ ϕ cos ⁡ ϕ - a cos 2 ⁡ θ sin ⁡ ϕ cos ⁡ ϕ ∂ φ ∂ θ × ∂ φ ∂ ϕ = - a 2 cos ⁡ θ sin 2 ⁡ ϕ ,   - a sin ⁡ θ sin 2 ⁡ ϕ ,   - a 2 sin ⁡ ϕ cos ⁡ ϕ ∂ φ ∂ θ × ∂ φ ∂ ϕ = - a 2 cos ⁡ θ sin 2 ⁡ ϕ 2 + - a sin ⁡ θ sin 2 ⁡ ϕ 2 + - a 2 sin ⁡ ϕ cos ⁡ ϕ 2 ∂ φ ∂ θ × ∂ φ ∂ ϕ = a 4 cos 2 ⁡ θ + sin 2 ⁡ θ sin 4 ⁡ ϕ + a 4 sin 2 ⁡ ϕ cos 2 ⁡ ϕ ∂ φ ∂ θ × ∂ φ ∂ ϕ = a 2 sin 2 ⁡ ϕ sin 2 ⁡ ϕ + cos 2 ⁡ ϕ ∂ φ ∂ θ × ∂ φ ∂ ϕ = a 2 sin ⁡ ϕ

Porém, sin ⁡ ϕ > 0 para o intervalo considerado para ϕ . Assim,

∂ φ ∂ θ × ∂ φ ∂ ϕ = a 2 sin ⁡ ϕ

Passo 4

Finalmente,

A = ∬ D ∂ φ ∂ θ × ∂ φ ∂ ϕ   d θ   d ϕ A = ∬ D a 2 sin ⁡ ϕ   d θ   d ϕ A = a 2 ∫ 0 α d θ   ∫ arccos ⁡ h / a π / 2 sin ⁡ ϕ   d ϕ A = a 2 α - cos ⁡ ϕ arccos ⁡ h / a π / 2 A = a 2 α - cos ⁡ π 2 + cos ⁡ arccos ⁡ h a A = a 2 α h a = a α h

Resposta

a α h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤
1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤
1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤
1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤
1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.) σ( u ,v )=( u ,v ,1-u-v ) ,u≥0 ,v≥0eu+v≤1 . σ( u ,v )=( u ,v ,2-u-v ) ,u 2+v 2 ≤1 . σ( u ,v )=( u ,v ,u 2+v 2 ) ,u 2+v 2≤