Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 1-e

1 ) Calcule a área. (Sugerimos ao leitor desenhar a imagem da superfíciedada.)

  1. σ   ( u ,   v )   =   ( u ,   v ,   1   -   u   -   v ) ,   u   ≥   0 ,   v   ≥   0   e   u   +   v   ≤   1 .
  2. σ   ( u ,   v )   =   ( u ,   v ,   2   -   u   -   v ) ,   u 2   +   v 2     ≤   1 .
  3. σ   ( u ,   v )   =   ( u ,   v ,   u 2   +   v 2 ) ,   u 2   +   v 2   ≤   4 .
  4. σ   ( u ,   v )   =   ( u ,   v ,   4   -   u 2   -   v 2 ) ,   ( u ,   v )   ∈   K , onde K é o conjunto no plano uv limitado pelo eixo u e pela curva (em coordenadas polares)

    5. ρ   =   e - θ     0   ≤   θ   ≤   π

  5. σ   u ,   v =   u ,   v , 1 2 u 2 ,     0 ≤   v   ≤   u   e   u ≤ 2
  6. σ   ( u   v )   =   ( c o s   u ,   v ,   s e n   u ) ,     u 2   +   4 v 2   ≤   1  

Passo 1

O primeiro passo é saber que superfície estamos trabalhando. A parametrização acima nos da

σ   u ,   v =   ( u ,   v , 1 2 u 2 )

Sob as condições

    0 ≤   v   ≤   u  

  u ≤ 2

Isso quer dizer que nossa região é um plano com formato de parabola

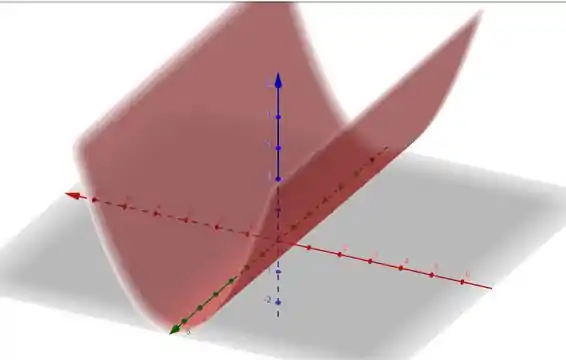
Passo 2

Quando quisermos calcular superfícies temos dois caminhos a seguir

∫ ∫ S d S =     ∫ ∫ R ∂ r ∂ u × ∂ r ∂ v   d u d v    

Ou

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Isso quer dizer que podemos: Parametrizar e calcular a área a partir daí. Projetar no num plano coordenado a superfície e calcular a área nessa superfície. Vou escolher a opção 2.

Passo 3

∫ ∫ S d S =     ∫ ∫ R ' 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Onde nosso z é

z = 1 2 u 2

Isso nos dá derivadas parciais da seguinte forma

z u =   u

z v =   0

Agora vamos jogar nossos dados na integração

∫ ∫ R ' 1 + ∂ z ∂ u 2 + ∂ z ∂ v 2 d u d v

=   ∫ ∫ R ' 1 + u 2 + 0 2 d u d v

Agora só precisamos encontrar os intervalos de integração. Lembra das condições iniciais? Então serão elas que nos dirão limites de integração

    0 ≤   v   ≤   u  

  u ≤ 2

Assim nossa integral fica

∫ 0 2   ∫ 0 u   1 + 4 u 2       d v d u

Integrando em v temos

∫ 0 2   1 + 4 u 2 u     d u

Essa integral já fizemos em outros exercícios. E tem como resultado

1 12 1 + 4 u 2 3 / 2 0 2

= 1 12   17 3 2 - 1

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ S d S =     1 12   17 3 2 - 1  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja S o cubo com vértices ± 1 , ± 1 , ± 1 . Aproxime ∫ ∫ S x 2 + 2 y 2 + 3 z 2d S usando as somas de Riemann como na Definição 1, tomando os retalhos S i j como os quadrados que são as faces do cubo
Encontrar a área da superfície do plano 2 x + y + 2 z = 16 , interceptado por x = 0 ,y = 0 ,x = 2 e y = 3 x = 0 ,y = 0 e x 2 + y 2 = 36 , no 1° octante
Calcular a área da superfície do paraboloide y = 3 - ( x 2 + z 2 ) interceptado pelo plano y = 0
Calcular a área da superfície plana 2 x + 2 y + 3 z = 6 , tomada no 1 ° octante.
Calcular a área da parte do cone z 2 = x 2 + y 2 que está no interior do paraboloide z = 2 x 2 + 2 y 2 .