Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.4 - Ex. 1c

Calcule a área da superfície gerada pela rotação, em torno do eixo x, do gráfico da função dada.

c) f x = x 2 , 0 ≤ x < 1 2

Passo 1

Para o calcular a área da superfície gerada pela rotação em torno do eixo precisamos aplicar a seguinte formula:

A x = 2 π ∫ b a f x 1 + f ' x 2 d x

Sendo f x = x 2 , vamos calcular sua derivada!

f ' x = 2 x

Passo 2

Substituindo f ' x :

A x = 2 π ∫ 0 1 2 x 2 1 + 4 x 2 d x

O bizu para calcular a primitiva desta integral é usar a substituição trigonométrica, me acompanhe, my friend!

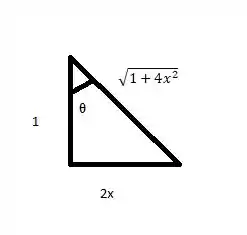
Vamos usar este triangulo para nos ajudar a fazer as substituições trigonométricas, dele podemos observar varias informações uteis, vamos por ordem:

1 ° )   tan ⁡ θ = 2 x , desta equação eu obtenho que :

x 2 = tan 2 ⁡ θ 4

d x = sec 2 ⁡ θ d θ 2

Ainda desta equação podemos obter o nosso novo intervalo em função de θ :

Veja que quando x = 0 = = > 2 0 = tan ⁡ θ   = = >   θ = 0

Analogamente x = 1 2 = = > 2 1 2 = tan ⁡ θ = = >   θ = π 4

Logo nosso intervalo será de 0≤   θ < π 4

2 ° ) sec ⁡ θ = 1 + 4 x 2

Passo 3

Agora que já sabemos tanto sobre nossa integral vamos calcula-la!

A x = 2 π ∫ 0 π 4 tan 2 ⁡   θ 4 sec ⁡   θ   sec 2 ⁡   θ d   θ 2  

A x = π 4 ∫ 0 π 4 tan 2 ⁡   θ sec 3 ⁡   θ d   θ

Lembrando que tan 2 ⁡   θ = sec 2 ⁡   θ - 1 , podemos quebrar nossa integral em duas :

A x = π 4 ∫ 0 π 4 sec 5 ⁡   θ d   θ - ∫ 0 π 4 sec 3 ⁡   θ d   θ

Passo 4

Vamos calcular estas integrais separadamente para evitar quaisquer tipos de erros , ok?!

1 ° )   ∫ 0 π 4 sec 3 ⁡   θ d   θ

u = s e c   θ                   d u = sec ⁡ θ tan ⁡   θ d   θ

d v = sec 2 ⁡   θ             v = tan ⁡   θ

∫ sec 3 ⁡   θ d   θ = t a n   θ s e c   θ - ∫ tan 2 ⁡ θ s e c   θ d   θ

Usando que tan 2 ⁡   θ = sec 2 ⁡   θ - 1 , chegaremos em :

∫ sec 3 ⁡   θ d   θ = 1 2 t a n   θ s e c   θ + ln ⁡ tan ⁡ θ + sec ⁡ θ + C

Agora que sabemos a primitiva vamos calcular a sua definida:

∫ 0 π 4 sec 3 ⁡   θ d   θ = 1 2 t a n π 4 s e c   π 4 + ln ⁡ tan ⁡ π 4 + sec ⁡ π 4 - 1 2 t a n   0 s e c   0 + ln ⁡ tan ⁡ 0 + sec ⁡ 0

∫ 0 π 4 sec 3 ⁡   θ d   θ = 1 2 2 + ln ⁡ 2 + 1 - 1 2 0 + ln ⁡ 1

∫ 0 π 4 sec 3 ⁡   θ d   θ = 1 2 2 + ln ⁡ 2 + 1

Passo 5

2 ° )   ∫ 0 π 4 sec 5 ⁡   θ d   θ

u = sec 3 ⁡ θ                     d u = 3 sec 3 ⁡ θ tan ⁡   θ d   θ

d v = sec 2 ⁡   θ             v = tan ⁡   θ

∫ sec 5 ⁡   θ d   θ = tan ⁡ θ sec 3 ⁡ θ - 3 ∫ sec 3 ⁡ θ tan 2 ⁡ θ d θ

Usando que tan 2 ⁡   θ = sec 2 ⁡   θ - 1 , chegaremos em :

∫ sec 5 ⁡   θ d   θ = 1 4 tan ⁡ θ sec 3 ⁡ θ - 3 4 ∫ sec 3 ⁡ θ d θ

Calculado a definida, note que podemos aproveitar o resultado do passo anterior!

∫ 0 π 4 sec 5 ⁡   θ d   θ =   1 4 tan ⁡ θ sec 3 ⁡ θ ] π 4 0 + ∫ 0 π 4 sec 3 ⁡   θ d   θ

∫ 0 π 4 sec 5 ⁡   θ d   θ = 1 8 7 2 + 3 ln ⁡ 2 + 1

Passo 6

Finalmente, calcularemos a nossa área, você ainda lembra dela né ?

A x = π 4 ∫ 0 π 4 sec 5 ⁡   θ d   θ - ∫ 0 π 4 sec 3 ⁡   θ d   θ

A x = π 4 1 8 7 2 + 3 ln ⁡ 2 + 1 - 1 2 2 + ln ⁡ 2 + 1

A x = π 32 3 2 - ln ⁡ 2 + 1

Resposta

A x = π 32 3 2 - ln ⁡ 2 + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a)Escreva uma integral para área da superfície obtida pela rotação da curva em torno do (i) eixo x e (ii) eixo y .(b) Use o recurso de integração numérica de sua calculadora para calcular as áreas da
(a)Escreva uma integral para área da superfície obtida pela rotação da curva em torno do (i) eixo x e (ii) eixo y .(b) Use o recurso de integração numérica de sua calculadora para calcular as áreas da
Use a regra de Simpson com n = 10 para estimar a areada superfície obtida pela rotação da curva em torno do eixo x . Compare a sua resposta com o valor fornecido pela sua calculadora. y = x ln ⁡ x,1 ≤
Calcule a área exata da superfície obtida pela rotação da curva em torno do eixo x . y = 1 + e x , 0 ≤ x ≤ 1
(a)Escreva uma integral para área da superfície obtida pela rotação da curva em torno do (i) eixo x e (ii) eixo y .(b) Use o recurso de integração numérica de sua calculadora para calcular as áreas da