Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.8 - Ex. 1

Calcule o comprimento da curva dada em coordenadas polares:

ρ =   θ   ,   0   ≤   θ   ≤ π

Passo 1

Sabemos que a fórmula para o comprimento de curvas em coordenadas polares é:

∫ a b ρ 2 +   d ρ d θ 2 d θ

Logo:

ρ ² =   θ ²

d ρ d θ = 1

Passo 2

Substituindo na integral e substituindo os limites de integração que são dados no problema:

∫ 0 π θ 2 +   1 2 d θ

Temos uma integral trigonométrica

Para que o teta da integral não se misture com o da questão, trocaremos por x.

∫ x 2 +   1 2 d x

Estamos no caso II, logo:

∫ x 2 +   1 2 d x = ∫ t g ( θ ) 2 +   1 2 d x

Devemos trocar o dx por d θ ,   logo, derivando x = 1tg( θ ) e dx = sec² θ d θ

∫ t g ( θ ) 2 +   1 2 d x = ∫ t g θ 2 +   1 2 s e c ² ( θ ) d θ

Também sabemos que tg²( θ ) + 1 = s e c ² ( θ )

∫ t g θ 2 +   1 2 s e c ² ( θ ) d θ =   ∫ s e c ² ( θ ) s e c ² ( θ ) d θ = ∫ s e c ² ( θ ) * s e c ( θ ) d θ = ∫ s e c ³ ( θ ) d θ

Mas, sabemos que ∫ s e c 3 x d x = 1 2 sec ⁡ x t g x + 1 2 l n ⁡ sec ⁡ x + t g x

Passo 3

O próximo passo é voltar para a variável x. Se x = tg( θ ):

Logo, escrevendo o resultado da integral em função de x:

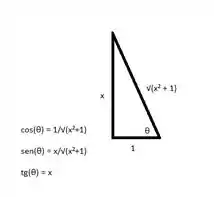
1 2 sec ⁡ x t g x + 1 2 ln ⁡ sec ⁡ x + t g x =   x 2 + 1 x 2 x 2 + 1 + 1 2 l n ⁡ ( x +   x 2 + 1 )

Aplicando-se os limites de integração teremos:

π 2 π 2 + 1 + 1 2 l n ⁡ ( π +   ( π 2 + 1 ) )

Resposta

O comprimento vale   π 2 π 2 + 1 + 1 2 l n ⁡ ( π +   ( π 2 + 1 ) )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-10, determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são.8- y = x 3 3 + x 2 + x + 1 4 x + 4 ,0 ≤ x ≤
27- Existe uma curva lisa y = f ( x ) (continuamente derivável) cujo comprimento ao longo do intervalo 0 ≤ x ≤ a seja sempre 2 a ? Justifique sua resposta.
23- Comprimento de um segmento de reta Use a fórmula de comprimento de arco (Equação 3) para determinar o comprimento do segmento de reta y = 3 - 2 x , 0 ≤ x ≤ 2 . Verifique sua resposta determinando
Nos Exercícios 1-10, determine o con1primento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são.4- x = y 3 2 3 - y 1 2d e y = 1ay = 9
24- Circunferência de um círculo Estabeleça uma integral para determinar a circunferência de um círculo de raio r centrado na origem. Você aprenderá a calcular a integral na Seção 8.3