Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.6 - Ex. 4

Calcule o comprimento da curva definida por σ t = t , 1 - t 2 , 1 do ponto 0,1 , 1 ao ponto 1,0 , 1 .

Passo 1

Fala galera, tudo show de bola? Pra começar, como a fórmula do comprimento da curva é:

L C = ∫ t o t f σ ' t   d t

Podemos encontrar os limites de integração. Note que como estamos indo do ponto 0,1 , 1 ao ponto 1,0 , 1 e σ t = t , 1 - t 2 , 1 , a coordenada x já nos dá os limites de integração. Seja o substiro " o " representando o valor inicial e o subscrito " f " representando o valor final:

x t = t

x t o = t o = 0

x t f = t f = 1

E logo:

L C = ∫ 0 1 σ ' t   d t

Agora, derivando σ t e calculando a norma, chegamos a:

σ ' t = 1 , - 2 t , 0

σ ' t = 1 2 + - 2 t 2 + 0 2

σ ' t = 1 + 4 t 2

Logo:

L C = ∫ 0 1 1 + 4 t 2   d t

Passo 2

Pra resolver esse carinha, vamos ter que fazer uma substituição trigonométrica. Usando o triângulo auxiliar:

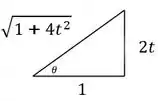
Temos que:

tg ⁡ θ = 2 t

t = 1 2 tg ⁡ θ

E tái nossa substituição. Derivando, chegamos a:

d t = 1 2 sec 2 ⁡ θ   d θ

Ainda do círculo, tiramos que:

cos ⁡ θ = 1 1 + 4 t 2

1 cos ⁡ θ = 1 + 4 t 2

1 + 4 t 2 = sec ⁡ θ

Ignorando por enquanto os limites de integração, integramos e obtemos:

∫ 1 + 4 t 2   d t = 1 2 ∫ sec 3 ⁡ θ   d θ  

Essa integral é um pouco complicada de resolver. Pra começar, vamos precisar fazer uma integração por partes. Seja:

∫ sec 3 ⁡ θ   d θ = ∫ sec ⁡ θ sec 2 ⁡ θ   d θ

Pela integração por partes, temos:

∫ u   d v = u v -   ∫ v   d u

Escolhendo

u = sec ⁡ θ

d v = sec 2 ⁡ θ   d θ

Derivando em cima e integrando em baixo:

d u = sec ⁡ θ   tg ⁡ θ   d θ

v = tg ⁡ θ

E logo:

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tg ⁡ θ -   ∫ sec ⁡ θ tg 2 ⁡ θ   d u

Parece que complicou, mas vamos lembrar da seguinte propriedade trigonométrica:

tg 2 ⁡ θ = sec 2 ⁡ θ - 1

E aplicando ela na segunda integral:

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tg ⁡ θ -   ∫ sec ⁡ θ sec 2 ⁡ θ - 1   d u

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tg ⁡ θ -   ∫ sec 3 ⁡ θ - sec ⁡ θ   d u

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tg ⁡ θ -   ∫ sec 3 ⁡ θ   d u + ∫ sec ⁡ θ   d u

2 ∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tg ⁡ θ + ∫ sec ⁡ θ   d u

∫ sec 3 ⁡ θ   d θ = 1 2 sec ⁡ θ tg ⁡ θ + ∫ sec ⁡ θ d u

A integral que sobrou é uma integral de resolução direta. Fechamos então:

∫ sec 3 ⁡ θ   d θ = 1 2 sec ⁡ θ tg ⁡ θ + ln ⁡ sec ⁡ θ + tg ⁡ θ

Como:

∫ 1 + 4 t 2   d t = 1 2 ∫ sec 3 ⁡ θ   d θ  

Temos:

∫ 1 + 4 t 2   d t = 1 4 sec ⁡ θ tg ⁡ θ + ln ⁡ sec ⁡ θ + tg ⁡ θ  

Do triângulo auxiliar, tiramos:

sec ⁡ θ = 1 + 4 t 2

tg ⁡ θ = 2 t

E logo:

∫ 1 + 4 t 2   d t = 1 4 2 t 1 + 4 t 2 + ln ⁡ 2 t + 1 + 4 t 2  

Passo 3

Esse é o passo final e partimos pro abraço em! Basta aplicarmos agora os limites de integração:

L C = ∫ 0 1 1 + 4 t 2   d t

L C = 1 4 2 t 1 + 4 t 2 + ln ⁡ 2 t + 1 + 4 t 2 0 1

L C = 1 4 2 1 + 4 + ln ⁡ 2 + 1 + 4 - 0 + ln ⁡ 0 + 1

L C = 1 4 2 5 + ln ⁡ 2 + 5 - 0 + ln ⁡ 1

L C = 2 5 + ln ⁡ 2 + 5 4

Resposta

L C = 2 5 + ln ⁡ 2 + 5 4       u . c .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o comprimento do arco das seguintes curvas:d) y = x 3 / 2 , z = 0 de P 0 0,0 , 0 a P 1 4,8 , 0
Escreva a função comprimento de arco de:c) r → t = t ,t 2
Verificar se as curvas dadas estão parametrizadas pelo comprimento de arco: h → s = s 2 , s 2 ,s ≥ 0
Verificar se as curvas dadas estão parametrizadas pelo comprimento de arco: r → t = 2 t - 1 ,t + 2 ,t ,t ≥ 0
Verificar se as curvas dadas estão parametrizadas pelo comprimento de arco: r → t = s e n t ,c o s t ,t ≥ 0