Primeiro precisamos Montar a integral que descreve o comprimento do gráfico, como sabemos ela é:
Assim a primeira coisa a se fazer é achar a derivada da função, que é:
Agora substituímos:
Passo 2
Essa equação tem cara de algo conhecido, a equação de cima() parece que vem de Pitágoras.
Repara nesse triângulo:
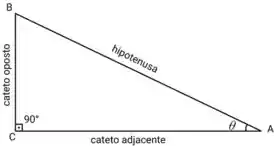
Se os lados dele fossem:
, e
Teríamos por consequência, que a f(x) na equação seria:
E:
Assim, substituindo, temos:
Analisando essa nova equação pode ser difícil de fazer por outros métodos, mas por acaso temos a relação já dada que
E isso nos remete a Integração por partes:
Reescrevendo a relação, temos:
Por consequência:
Substituindo:
Se
Logo:
Voltando pra coordenada x:
Passo 3
Agora voltamos aos limites de integração:
