Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.4 - Ex. 3d

Calcule o comprimento do gráfico da função dada.

f (x) = sqrt(x) , (1)/(4) <= x <= (3)/(4)

Passo 1

Como provado na questão 2 o comprimento de uma função f ( x ) no intervalo x in [a , b] é dado por

L = int_a^b sqrt(1 + [f^' (x)]^2) d x

Então, derivando a função

f^' (x) = (1)/(2 sqrt(x))

E o comprimento é dado por

L = int_(1 // 4)^(3 // 4) sqrt(1 + [(1)/(2 sqrt(x))]^2) d x = int_(1 // 4)^(3 // 4) sqrt(1 + (1)/(4 x)) d x

Passo 2

Resolvendo a integral

int_(1 // 4)^(3 // 4) sqrt(1 + (1)/(4 x)) d x = int_(1 // 4)^(3 // 4) sqrt((4 x + 1)/(4 x)) d x

Vamos esquecer os limites por enquanto.

int sqrt((4 x + 1)/(4 x)) d x

Vamos utilizar a integração por partes

int f * g^' d x = f * g - int f^' * g d x

Neste caso nossas funções são

{[[f = sqrt((4 x + 1)/(4 x))],[g^' = 1]]) -> (f^' = (1)/(2 sqrt((4 x + 1)/(4 x))) (4 (4 x) - ( 4 x + 1 ) 4)/((4 x)^2) = (- 1)/(8 x^2 sqrt((4 x + 1)/(4 x))))/(g = x)

E temos

int sqrt((4 x + 1)/(4 x)) d x = x sqrt((4 x + 1)/(4 x)) + int (d x)/(8 x sqrt((4 x + 1)/(4 x)))

Passo 3

Olhando então para essa nova integral

int (d x)/(8 x sqrt((4 x + 1)/(4 x)))

Vamos manipular um pouco

= int (sqrt(4 x) d x)/(8 x sqrt(4 x + 1)) = int (2 sqrt(x) d x)/(8 x sqrt(4 x + 1))

= (1)/(4) int (d x)/(sqrt(x) sqrt(4 x + 1))

Aplicando a substituição

{[[u = sqrt(x)],[d u = (1)/(2 sqrt(x)) d x]])

= (1)/(4) int (2 d u)/(sqrt(4 u^2 + 1))

Utilizando então a substituição trigonométrica

{[[2 u = tg alpha => 4 u^2 = tg^2 alpha],[2 d u = sec^2 alpha d alpha]])

= (1)/(4) int (sec^2 alpha d alpha)/(sqrt(tg^2 alpha + 1)) = (1)/(4) int (sec^2 alpha d alpha)/(sqrt(tg^2 alpha + 1))

= (1)/(4) int (sec^2 alpha d alpha)/(sec alpha) = (1)/(4) int sec alpha d alpha

= (1)/(4) ln (sec alpha + tg alpha) + C

Retornando as variáveis anteriores, utilizando o triangulo:

= (1)/(4) ln (sqrt(4 u^2 + 1) + 2 u) + C

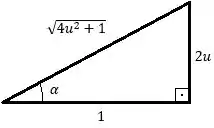
E temos

int (d x)/(8 x sqrt((4 x + 1)/(4 x))) = (1)/(4) ln (sqrt(4 x + 1) + 2 sqrt(x)) + C

Portanto

int sqrt((4 x + 1)/(4 x)) d x = x sqrt((4 x + 1)/(4 x)) + (1)/(4) ln (sqrt(4 x + 1) + 2 sqrt(x)) + C

Passo 4

Retornando os limites de integração

int_(1 // 4)^(3 // 4) sqrt((4 x + 1)/(4 x)) d x = [x sqrt((4 x + 1)/(4 x)) + (1)/(4) ln (sqrt(4 x + 1) + 2 sqrt(x))]_((1)/(4))^((3)/(4))

= [(3)/(4) sqrt((3 + 1)/(3)) + (1)/(4) ln (sqrt(3 + 1) + 2 sqrt((3)/(4)))] - [(1)/(4) sqrt((1 + 1)/(1)) + (1)/(4) ln (sqrt(1 + 1) + 2 sqrt((1)/(4)))]

= (sqrt(3))/(2) + (1)/(4) ln (2 + sqrt(3)) - (sqrt(2))/(4) - (1)/(4) ln (sqrt(2) + 1)

= (sqrt(3))/(2) - (sqrt(2))/(4) + (1)/(4) ln ((2 + sqrt(3))/(1 + sqrt(2)))

Resposta

(sqrt(3))/(2) - (sqrt(2))/(4) + (1)/(4) ln ((2 + sqrt(3))/(1 + sqrt(2)))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície lateral (lado) do cone gerado pela rotação do segmento de reta y = x 2 , 0 ≤ x ≤ 4 , em torno do eixo x . Verifique se sua resposta coincide com a fórmula geométrica.Áre
Determine a área da superfície lateral do cone gerado pela rotação do segmento de reta y = x 2,0 ≤ x ≤ 4 , em torono do eixo y . Verifique se seu resultado coincide com a fórmula geométrica: Á r e ad
Determine a área da superfície do tronco de cone gerado pela rotação do segmento de reta y = x 2 + 1 2 , 1 ≤ x ≤ 3 , em torno do eixo x . Verifique se sua resposta coincide com a fórmula geométrica. Á
Determine a área da superfície do tronco de cone gerado pela rotação do segmento de reta y = x 2 + 1 2,1 ≤ x ≤ 3 , em torono do eixo y . Verifique se seu resultado coincide com a fórmula geométrica: Á
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = x 3 9 , 0 ≤ x ≤ 2 ;e i x ox