Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 2d
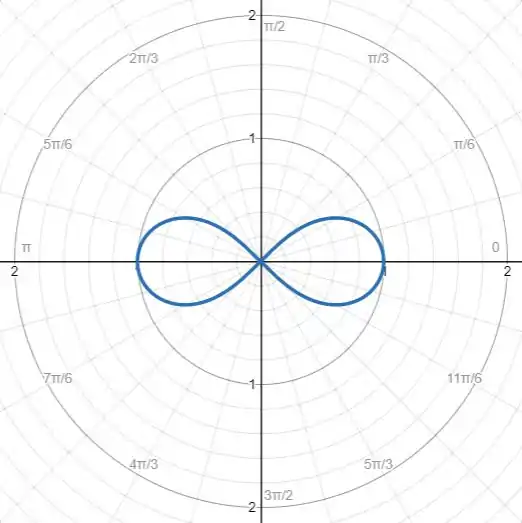
Passe a curva dada para coordenadas polares e desenhe-a.
Passo 1
Utilizando a substituição
Para transformar a equação para coordenadas polares
Passo 2
Montando a tabelinha de e , com os ângulos principais:
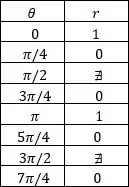
Podemos perceber que nos intervalos e a função não assume valor real, já que é negativos nesses intervalos e não podemos aplicar a raiz, portanto nesses intervalos não temos curvas.
Passo 3
Com os valores que encontramos e as análises feitas, podemos esboçar o gráfico de
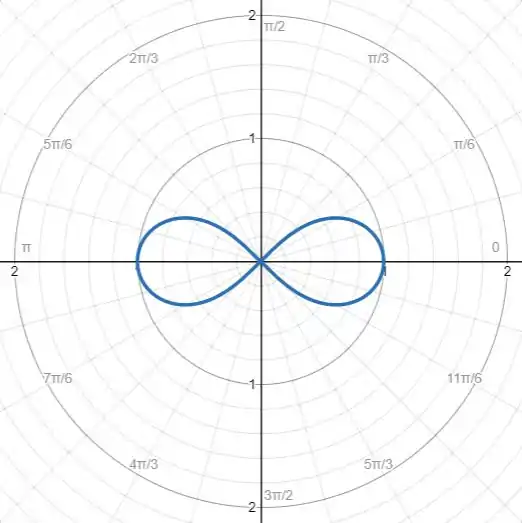
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa da área da região que está sob a curva dada. A seguir, encontre a área exata. y = 2 x + 1 , 0 ≤ x ≤ 1
Use um gráfico para dar uma estimativa da área da região que está sob a curva dada. A seguir, encontre a área exata. y = 2s e nx - s e n2 x , 0 ≤ x ≤ π
Esboce a região delimitada pelas curvas dadas. Decida quando integrar com relação a x ou a y . Desenhe um retângulo aproximante e coloque sua altura e largura. Então calcule a área da região.
Calcule a integral e interprete-a como uma diferença de áreas. Ilustre com um esboço ∫ - 1 2 x 3 d x
Calcule a integral e interprete-a como uma diferença de áreas. Ilustre com um esboço ∫ π 4 5 π 2 sin x d x