Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.8 - Ex. 2
Calcule nos exercícios abaixo:
e é o triângulo de vértices , e , onde o vetor normal tem componente não negativa.
Passo 1
Bom galera, o exercício nos pede para calcular e nos dá as informações de que e que
: triângulo de vértices , e ,
com vetor normal exterior com componente .
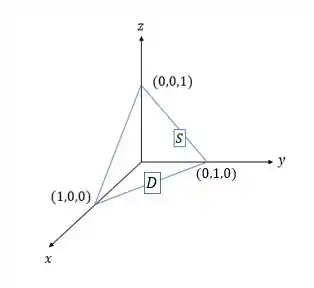
Olhando para o plano , nós temos , observe:
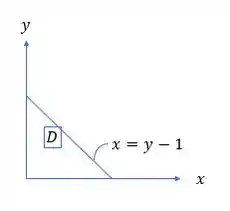
Logo, o intervalo de convergência é dado por:
Assim,
Passo 2
Já podemos montar nossa integral:
Passo 3
Resolvendo a integral de dentro:
Passo 4
Agora, resolvendo a integral de fora:
Resposta
Exercícios de Livros Relacionados
Calcular I =∫ ∫ S x 2 d y d z + y 2 d z d x + z 2 d x d y Onde S é a superfície exterior da semi-esfera x 2 + y 2 + z 2 = a 2 ,z ≥ 0
Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
Calcular ∫ ∫ S f → *n →d S Sendo f → = xi → + yj → +z k → e S a parte do plano 2 x + 3 y + 4 z = 12 cortada pelos planos x= 0 ,y = 0 ,x = 1 ,y = 2 e n → é a normal com componente z não negativa
Um fluido tem um vetor densidade de fluxo f → = x i → - 2 x + y j → + k .→ Sejam S hemisfério x ² + y ² + z ² = 4 ² ² ² , z ≥ 0 e n → a normal que aponta para fora . Calcular a massa de fluido que atr