Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.7 - Ex. 4

Calcule ∮ C y x 2 d x - x 3 d y x 2 + y 2 2 , onde C é a curva dada pela equação x 2 4 + y - 1 3 2 = 1 , percorrida no sentido anti-horário.

Passo 1

Okay, vamos lá resolver essa questão?!

A nossa curva é uma elipse do seguinte formato:

Numa curva fechada podemos usar Green, certo?! Mas olha só.

O nosso campo é F x , y = y x 2 x 2 + y 2 2 , - x 3 x 2 + y 2 2 . Mas cara, veja bem, esse campo não está definido para ( 0,0 ) , daí, não poderemos usar Green nesse caso, porque teríamos um buraco no campo. Mas e se a gente adicionasse uma outra curva ali, assim ó:

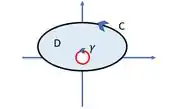
Daí,

∮ C ∪ γ - F d r = ∬ D δ F 2 δ x - δ F 1 δ y d x d y

Passo 2

Agora olha só, temos:

δ F 2 δ x = x 2 - 3 y 2 x 2 + y 2 3

δ F 1 δ y = x 2 - 3 y 2 x 2 + y 2 3

Assim,

δ F 2 δ x - δ F 1 δ y = 0

Logo,

∮ C ∪ γ - F d r = 0 ∴ ∮ C F d r + ∮ γ - F d r = 0 → ∮ C F d r = ∮ γ F d r

Note que a integral de γ passa negativa, só que, alterando sua orientação, mudamos também o seu sinal.

Passo 3

Temos então que nossa integral será igual a integral da curva que adicionamos dentro da elipse, no caso, adicionamos uma circunferência de raio a qualquer, assim, parametrizando γ :

γ : x 2 + y 2 = a 2

σ θ = a cos ⁡ θ , a sen ⁡ θ       0 ≤ θ ≤ 2 π

σ ' θ = ( - a s e n   θ , acos ⁡ θ )

Escolhemos uma circunferência pois ela se adepta perfeitamente ao campo, olha só:

F σ θ = a 3 sen ⁡ θ cos 2 ⁡ θ a 2 sen 2 ⁡ θ + a 2 cos 2 ⁡ θ 2 , - a 3 cos 3 ⁡ θ a 2 sen 2 ⁡ θ + a 2 cos 2 ⁡ θ 2 = a 3 sen ⁡ θ cos 2 ⁡ θ a 2 ( sen 2 ⁡ θ + cos 2 ⁡ θ ) 2 , - a 3 cos 3 ⁡ θ a 2 ( sen 2 ⁡ θ + cos 2 ⁡ θ ) 2 = a 3 sen ⁡ θ cos 2 ⁡ θ a 4 , - a 3 cos 3 ⁡ θ a 4

Note que usamos uma relação trigonométrica onde, sen 2 ⁡ θ + cos 2 ⁡ θ = 1 , daí:

∮ C F d r = ∮ γ F d r = ∫ 0 2 π F σ θ σ ' θ d θ = ∫ 0 2 π a 3 sen ⁡ θ cos 2 ⁡ θ a 4 , - a 3 cos 3 ⁡ θ a 4 - a s e n   θ , acos ⁡ θ = ∫ 0 2 π - cos 2 ⁡ θ d θ =   - ∫ 0 2 π 1 + cos ⁡ 2 θ 2 d θ = - π

Resposta

- π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais campos nos Exercícios 1-6 são conservativos e quais não são? F = y i + ( x + z ) j - y k
Quais campos nos Exercícios 1-6 são conservativos e quais não são? F = y z i + x z j + x y k
Quais campos nos Exercícios 1-6 são conservativos e quais não são? F = e x c o s ⁡ y i - e x s e n ⁡ y j + z k
Nos Exercícios 7-12, encontre uma função potencial ƒ para o campo F F = l n ⁡ x + s e c 2 ⁡ ( x + y ) i + s e c 2 ⁡ ( x + y ) + y y 2 + z 2 j + z y 2 + z 2 k
Nos Exercícios 27 e 28, encontre uma função potencial para F F = 2 x y i + 1 - x 2 y 2 j , { ( x , y ) : y0 }