Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 1

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva C .

∮ C y   d x + z d y + x d z = - 2 π 2

Onde C é a curva obtida como intersecção do plano x + y = 2 com a esfera x 2 + y 2 + z 2 = 2 x + y .

Passo 1

Faaalaaa meus queriidoos... Tudo em ordem por aí? Espero muito que sim. Vamos juntos aplicar o teorema do Tio Stokes. Bora!

Primeiramente, antes de mais nada, no abrir das cortinas, vamos tentar enxergar quem raios é a nossa curva C :

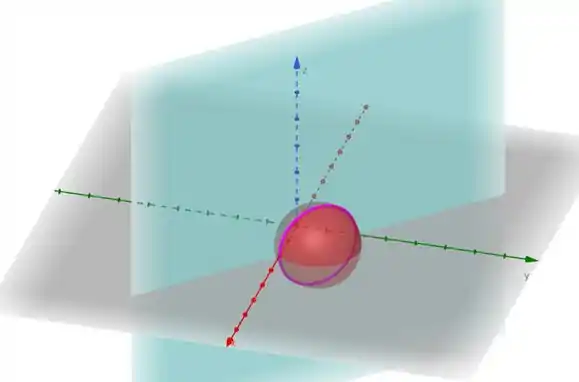
Teremos algo mais ou menos assim; de forma que aquele negocinho meio rosa ali é exatamente a curva C .

Vamos isolar essa curva só pra deixar menos poluído esse rolê:

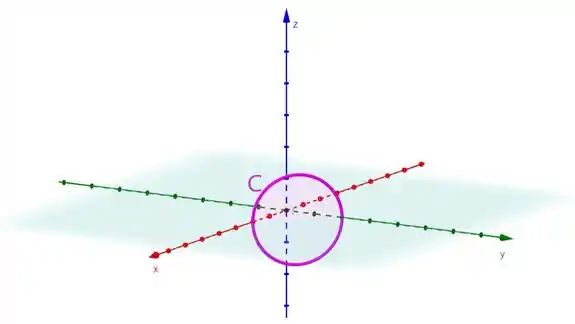
Tá beleza. Então o que temos que fazer é provar que:

∮ C y   d x + z d y + x d z = - 2 π 2

Mas usando o Teorema de Stokes. O que ele diz mesmo??? Vamo ver:

∮ C F → d r = ∬ S r o t F →   .     n →   d s = ∬ S r o t F →   .   N →   d u d v

Ou seja, ele transforma uma integral de linha em uma integral de superfície. Beleza, isso significa que antes de qualquer outra coisa, o que precisamos fazer é saber quem raios é a SUPERFÍCIE S .

A possibilidade mais simples é tomar a seguinte:

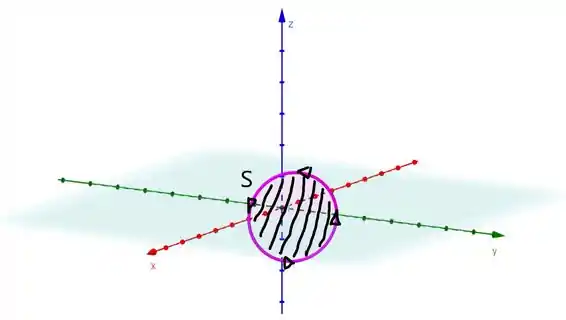
Percebeu a diferença entre a curva C e agora a nossa superfície S ?? Perceba também que já definimos uma orientação no sentido anti-horário para a borda da superfície.

Beleza, já temos a superfície vamos atrás dos bang que compõe a integral dupla.

Passo 2

Começando do rotacional, se você se lembrar bem ele é definido assim:

r o t F → = ∇   x   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3 = ∂ F 3 ∂ y - ∂ F 2 ∂ z   ;   ∂ F 1 ∂ z - ∂ F 3 ∂ x     ;   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Lembrando que o nosso campo está assim definido:

F → = ( y   ;   z   ;   x )

Ou seja, F 1 = y , F 2 = z e F 3 = x .

Dito isso, vamos obter esse cara então:

∂ F 3 ∂ y - ∂ F 2 ∂ z = 0 - 1 = - 1

∂ F 1 ∂ z - ∂ F 3 ∂ x = 0 - 1 = - 1

E

∂ F 2 ∂ x - ∂ F 1 ∂ y = 0 - 1 = - 1

Isso significa que:

r o t F → = - 1 ;   - 1 ;   - 1

Guarda essa informação aí. Seguindo:

Agora, para obter o n → que nada mais é do que o vetor normal a superfície, temos antes de qualquer outra coisa que parametrizar a curva...

Mas se você perceber, ser normal a superfície é ser normal ao plano, certo? Então tudo o que precisamos fazer é obter o vetor normal ao plano x + y = 2 .

Lembra que para um plano qualquer: a x + b y + c z = d o vetor normal será:

n → = a ; b ; c

Sacou a ideia? Então o nosso vetor normal será:

n → = 1   ; 1   ; 0

Agora você vai fazer o seguinte, voltando na imagem da superfície pegue sua mão direita e coloque na tela; faça o sinal de “jóia”. Os seus outros quatro dedos irão percorrer o sentido da curva (como se o seu pulso fosse o centro da circunferência); note então que o seu dedão está apontado para você.

Isso condiz com o resultado que acabamos de obter (primeiro quadrante do plano x y ). Conseguiu enxergar?

Shooow dibolla.

Passo 3

Perceba que até agora temos o seguinte:

∬ S r o t F →   .     n →   d s

Aplicando o que encontramos até agora:

∬ S - 1 ; - 1 ; - 1   .     1 ; 1 ; 0   d s

Chegamos em:

∬ S - 1 + - 1 + 0   d s

Então:

∬ S - 2 d s = - 2 ∬ S d s

Se você se lembrar,

∬ S d s = A r e a

Mas essa área é a da projeção dessa curva em algum plano. Você consegue enxergar qual o formato dessa projeção?? Para facilitar, podemos invocar a tia Mat olha só, a projeção no plano y z será dada pela intersecção da esfera com o plano; então:

x = 2 - y

E substituindo esse x na fórmula da esfera:

2 - y 2 + y 2 + z 2 = 2 2 - y + y

Ajeitando isso:

4 - 4 y + y 2 + y 2 + z 2 = 4

Portanto:

2 y 2 - 4 y + z 2 = 0

Dividindo isso por 2:

y 2 - 2 y + z 2 2 = 0

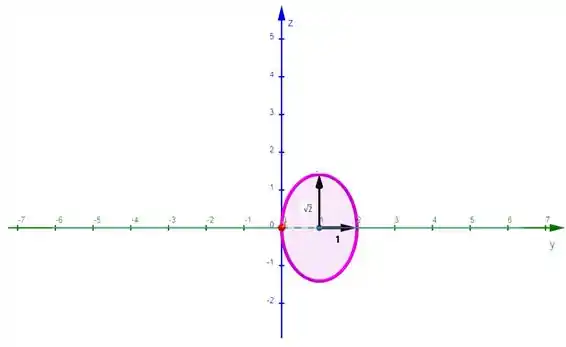
Repare que esse termo é o de uma elipse.... Consegue ver isso?? Talvez assim fique melhor de visualizar:

y - 1 2 + z 2 2 = 1

Uma elipse centrada em 1 ; 0 , que corta o eixo y nos pontos 0,0     e   2,0 e mais alongada no sentido de z . Olha só como fica:

Com isso:

∬ D d y d z = A r e a   e l i p s e

Lembra como achamos a area de uma elipse??? E a mesma ideia da circunferência, π vezes o raio, mas levando em consideração que a elipse tem “dois raios”:

A e l i p s e = a b π = 1   .   2   .   π = 2   π

Portanto:

∬ d y d z = 2   π

E

∬ S r o t F →   .     n →   d s = - 2   .   2   π = - 2 2  

That’s... See u.

Resposta

Demonstrado.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ C Fd r , Onde: F x , y , z = e - y - z e - x; e - z - x e - y; e - x - y e - z E C é a curva parametrizada: σ t = ln ⁡ 1 + t ln ⁡ 2; sin ⁡ π t 2; 1 - e t 1 - e Com 0 ≤ t ≤ 1 .
Calcule: ∫ C 2 x y z + sin ⁡ x d x + x 2 z + e y d y + x 2 y + 1 z d z Onde C é a curva parametrizada por: σ t = cos 3 ⁡ t; sin 2 ⁡ t ; t + 1 2 , 0 ≤ t ≤ π .
Calcule: ∫ C 4 x y - 3 x 2 z 2 d x + 2 x 2 d y - 2 x 3 zd z Onde C é a interseção da superfície: x 2 3 + y 2 4 + z 2 = 1 Com z ≥ 0 , com o plano y = 1 . Indique a orientação escolhida.
Use o Teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S → . F → x , y , z = 2 yc o s zi → + e xs e n zj → + x e y k → , S é o hemisfério x 2 + y 2 + z 2 = 9 ,z ≥ 0 , orientado para cima.
Como o teorema de Stokes generaliza o teorema de Green?