Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 11b

Calcule:

  1. O fluxo de F x , y , z = x 2 + y 2 + z 2 - 3 2 ( x , y , z ) através das faces do cubo W definido por

W = x , y , z ∈ R 3     |   - 1 ≤ x ≤ 1 , - 1 ≤ y ≤ 1 , - 1 ≤ z ≤ 1 .

Passo 1

Vamos nessa! Como o exercício pede o fluxo de F ( x , y , z ) através das faces do cubo centrado no ponto ( 0,0 , 0 ) , podemos logo de cara que estamos lidando com uma superfície fechada. Entretanto, o fluxo não está definido em F ( x , y , z ) .

Para diminuirmos a quantidade de integrais que teremos que resolver, podemos dizer que o módulo do fluxo através das faces do cubo é igual ao fluxo através da superfície de uma esfera localizada dentro do cubo centrada na origem.Veja o esboço da figura.

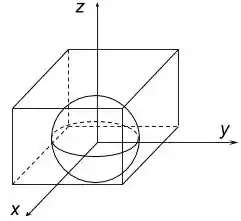
Podemos aproveitar o momento para definir as regiões de interesse.

S A : superfície da esfera com n A , i n t e r i o r

W : superfície do cubo

D : S A ∪ W

Passo 2

O fato das superfícies serem fechadas nos permite usar o Teorema de Gauss para calcular o fluxo. Este nos fornece que

∬ S F →     .   n →   d s = ∭ B d i v F → d V .

Onde

B : região entre a esfera e as faces do cubo

No nosso caso temos que

∭ B d i v F → d V = ∬ D F →     .   n →   d s = ∬ W F →     .   n → e x t e r i o r   d s + ∬ S A F →     .   n → A , i n t e r i o r   d s     ( 1 )

Passo 3

Agora podemos calcular o divergente.

d i v   F = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

Onde

∂ F 1 ∂ x = ∂ ∂ x x 2 + y 2 + z 2 - 3 / 2   x

∂ F 2 ∂ y = ∂ ∂ y x 2 + y 2 + z 2 - 3 / 2   y

∂ F 3 ∂ z = ∂ ∂ z x 2 + y 2 + z 2 - 3 / 2   z

Podemos calcular as derivadas percebendo que elas são do tipo

∂ ∂ x u v = v ∂ u ∂ x - u ∂ v ∂ x v 2  

Portanto

∂ F 1 ∂ x = ∂ ∂ x x x 2 + y 2 + z 2 = 1 . x 2 + y 2 + z 2 3 / 2 - 3 2 x 2 + y 2 + z 2 1 / 2 x   .   2 x x 2 + y 2 + z 2 3

= x 2 + y 2 + z 2 3 2   -   3 x 2 x 2 + y 2 + z 2 1 / 2 x 2 + y 2 + z 2 3

Podemos calcular os outros de forma análoga.

∂ F 2 ∂ y = x 2 + y 2 + z 2 3 2 -   3 y 2 x 2 + y 2 + z 2 1 / 2 x 2 + y 2 + z 2 3

∂ F 3 ∂ z = x 2 + y 2 + z 2 3 2 -   3 z 2 x 2 + y 2 + z 2 1 / 2 x 2 + y 2 + z 2 3

Podemos colocar x 2 + y 2 + z 2 3 2   em evidencia , assim teremos

d i v   F = x 2 + y 2 + z 2 3 2 ( 3 - 3 ) x 2 + y 2 + z 2 2 = 0 .

Assim, pela equação (1), podemos concluir que

∬ W F →     .   n → e x t e r i o r   d s + ∬ S A F →     .   n → A , i n t e r i o r   d s = 0

Portanto

∬ W F →     .   n → e x t e r i o r   d s = - ∬ S A F →     .   n → A , i n t e r i o r   d s .

Adotanto uma normal exteriot em S A , temos

∬ W F →     .   n → e x t e r i o r   d s = ∬ S A F →     .   n → A , e x t e r i o r   d s .

Passo 4

Vamos fazer a parametrização de S A usando coordenadas esféticas.

x = ρ s e n φ c o s θ y = ρ s e n φ s e n θ z = ρ c o s φ

Sendo assim, temos que o

F x , y , z ⟹ F ρ s e n φ c o s θ , ρ s e n φ s e n θ , ρ c o s φ = 1 ρ 3 ρ s e n φ c o s θ , ρ s e n φ s e n θ , ρ c o s φ

n A , e x t e r i o r = ρ 2 s e n φ ρ s e n φ c o s θ , ρ s e n φ s e n θ , ρ c o s φ

Onde

0 ≤ φ ≤ π

0 ≤ θ ≤ 2 π

Agora podemos montar a integral

∫ 0 2 π ∫ 0 π 1 ρ 3 ρ s e n φ c o s θ , ρ s e n φ s e n θ , ρ c o s φ ρ 2 s e n φ ρ s e n φ c o s θ , ρ s e n φ s e n θ , ρ c o s φ d φ d θ

Agora podemos simplificar a integral acima

∫ 0 2 π ∫ 0 π s e n 3 φ cos 2 ⁡ θ + s e n 3 φ s e n 2 θ + s e n φ cos 2 ⁡ φ   d φ d θ .

Podemos simplificar ainda mais usando a identidade trigonométrica cos 2 ⁡ a + s e n 2 a = 1 .

s e n 3 φ cos 2 ⁡ θ + s e n 2 θ + s e n φ cos 2 ⁡ φ = s e n φ cos 2 ⁡ φ + s e n 2 φ = s e n φ

Portanto a integral acima fica

∫ 0 2 π ∫ 0 π s e n φ   d φ d θ .

Passo 5

Agora precisamos calcular a integral acima.

∫ 0 2 π ∫ 0 π s e n φ   d φ d θ = ∫ 0 2 π - c o s φ 0 π d θ = ∫ 0 2 π 2 d θ = 2   × θ 0 2 π = 4 π .

Portanto

∬ S A F →     .   n → A , e x t e r i o r   d s = 4 π

Passo 6

Como vimos antes

∬ W F →     .   n → e x t e r i o r   d s = ∬ S A F →     .   n → A , e x t e r i o r   d s

Sendo assim

∬ W F →     .   n → e x t e r i o r   d s = 4 π .

Resposta

∬ W F →     .   n → e x t e r i o r   d s = 4 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o divergente do campo vetorial dado. u → x , y , z = x i → + y j → + z k →
Calcule o divergente do campo vetorial dado. F → x , y , z = x 2 - y 2 i → + s e n x 2 + y 2 j → + a r c t gzk →
Calcule o divergente do campo vetorial dado. F → x , y , z = x 2 + y 2 + z 2 a r c t gx 2 + y 2 + z 2 k →
Seja φ x , y = f x 2 + y 2 , onde f ( u ) é uma função real, de uma variável real e derivável até a 2ª ordem. Suponha que ∇ 2 φ = 0 .Mostre que uf ' ' u = - f ' u ,u0 .Determine uma f não constante, p
φ ( x , y ) é uma função cujo gradiente tem a representação geométrica abaixo:O que é mais razoável? ∇ 2 φ = 0o u∇ 2 φ ≠ 0 ?