Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.4 - Ex. 7
é uma função cujo gradiente tem a representação geométrica abaixo:
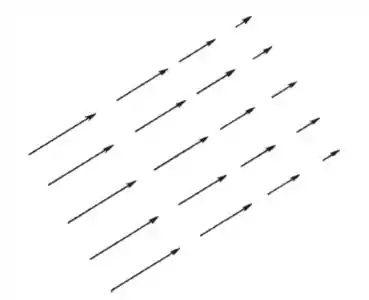
O que é mais razoável? ?
Passo 1
Bom, o gradiente da função tá representado na figura né? Então é o seguinte:
Tá tendo uma variação entre o tamanho dos vetores que seguem uma mesma linha né? Isso quer dizer que o divergente não é zero. Como o laplaciano é a derivada segunda do gradiente, e sabemos que o divergente não dá zero, é mais razoável pensarmos que não é?! Então é isso...
Resposta
Exercícios de Livros Relacionados
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S x d y d z + y d y d x + z d x d y Sendo S a parte da esfera x 2 + y 2 + z 2 = 1 abaixo do plano z = 1 / 2 , com normal ex
Verificar o teorema da divergência para f → = 2 x y + z i ^ + y 2 j ^ - x + 3 y k ^ Tomado no sólido limitado por x + y + 2 z = 6 ,x = 0 ,y = 0 e z = 0 .
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = x y i ^ + y z j ^ + x z k ^ e T o cone z ≥ x 2 + y 2 ,z ≤ 4
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = x 2 y , 2 x z , z 2 e S a superfície exterior do paralelepípedo retangular delimitado pelos pla
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = ( 0,0 , 2 z ) e S a superfície do Exercício 13, exceto a face superior.