Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 7

Calcule a integral

int_0^a (d x)/((a^2 + x^2)^((3)/(2))) , a > 0

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema queremos calcular a integral

int_0^a (d x)/((a^2 + x^2)^((3)/(2)))

Para a > 0 ...

Tem ideia de como fazemos isso? 🤔

Para simplificar nossa vida, podemos aplicar o método de substituição.

Dessa forma substituímos a variável de integração uma função que nos possibilite simplificar o cálculo da integral...

Olhando para a integral, como você acha que podemos substituir x ? 🤔

A tabela abaixo irá te ajudar:

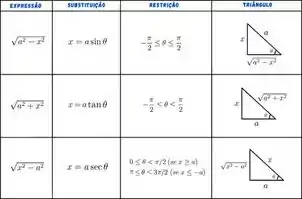
Passo 2

Vamos fazer a seguinte substituição

x = a t g theta

d x = a sec^2 theta

Mudando os limites de integração,

x = 0 => theta = 0

x = a => theta = (pi)/(4)

Substituindo na integral,

int_0^a (d x)/((a^2 + x^2)^((3)/(2))) = int_0^((pi)/(4)) (a sec^2 theta d theta)/([a^2 (1 + t g^2 theta)]^((3)/(2)))

Ajeitando as contas,

int_0^((pi)/(4)) (a sec^2 theta d theta)/([a^2 (1 + t g^2 theta)]^((3)/(2)))

= int_0^((pi)/(4)) (a sec^2 theta d theta)/(a^3 sec^3 theta)

= (1)/(a^2) int_0^((pi)/(4)) cos theta d theta

Pelo teorema fundamental do cálculo, temos

(1)/(a^2) int_0^((pi)/(4)) cos theta d theta = (1)/(a^2) [s e n theta]_0^((pi)/(4))

Aplicando os limites de integração,

(1)/(a^2) [s e n theta]_0^((pi)/(4)) = (1)/(a^2) ((sqrt(2))/(2) - 0)

Portanto, chegamos em

int_0^a (d x)/((a^2 + x^2)^((3)/(2))) = (1)/(sqrt(2) a^2)

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

int_0^a (d x)/((a^2 + x^2)^((3)/(2))) = (1)/(sqrt(2) a^2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integralint (x + a r c s e n x)/(sqrt(1 - x^2)) d x
Use a entrada indicada na Tabela de Integrais no fim do livro para calcular a integral. ∫ 7 - 2 x 2 x 2 d x ; e n t r a d a33
Utilize a tabela de integrais no fim do livro para calcular a integral ∫ 0 2 x 3 4 x 2 - x 4 d x
Utilize a tabela de integrais no fim do livro para calcular a integral ∫ y 6 + 4 y - 4 y 2 d y
Utilize a tabela de integrais no fim do livro para calcular a integral ∫ 4 + ln ⁡ x 2 x d x