Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.5 - Ex. 73

Calcule a integral

int (x + a r c s e n x)/(sqrt(1 - x^2)) d x

Passo 1

Bom galera, nesse exercício iremos utilizar as técnicas de integração estudadas e as estratégias abordadas nesse capítulo para resolver a integral. Dessa forma, queremos encontrar o resultado para a integral da maneira mais prática de acordo com as técnicas de integração deste capítulo.

Passo 2

Utilizando a seguinte substituição trigonométrica, temos

x = s e n theta ; theta = a r c s e n theta ; d theta = (1)/(sqrt(1 - x^2))

int (x + a r c s e n x)/(sqrt(1 - x^2)) d x = int ( s e n theta + theta ) d theta

Passo 3

Resolvendo a integral, temos

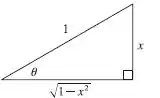
int ( s e n theta + theta ) d theta = - cos theta + (theta^2)/(2) + C

Utilizando o seguinte triângulo, podemos voltar para x

- cos theta + (theta^2)/(2) + C = - sqrt(1 - x^2) + ((s e n^(- 1) x)^2)/(2) + C

Resposta

int (x + a r c s e n x)/(sqrt(1 - x^2)) d x = - sqrt(1 - x^2) + ((s e n^(- 1) x)^2)/(2) + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida: ∫ sec 2 ⁡ x d x 4 - tan 2 ⁡ x 3 2
Calcule a integral indefinida: ∫ e - x d x 9 e - 2 x + 1 3 2
Calcule a integral indefinida: ∫ ln 3 ⁡ w d w wln 2 ⁡ w - 4
Calcule a integral indefinida: ∫ d z z 2 - 6 z + 18 3 2
Calcule a integral indefinida: ∫ 16 - e 2 x e x d x