Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 37
Calcule a integral.
Passo 1
E aí, pessoal!
Nesse problema temos que calcular a integral
Parece complicado?
Para resolver esse problema podemos simplificar nossa função de integração para podermos aplicar o teorema fundamental do calculo.
Para a simplificação só precisamos relembrar que:
Agora para calcular a integral devemos calcular primeiro a indefinida para encontrar a primitiva e, depois, aplicar o Teorema Fundamental do Cálculo, que diz o seguinte:
Que a integral definida é tipo medir a área sob a curva de entre dois pontos, digamos e . É como calcular o espaço que a função ocupa no gráfico.
Aqui vem o truque! Se você conhece uma antiderivada de , a integral definida de entre e é igual a . Ou seja, a diferença entre os valores da antiderivada nos pontos e .
Fica dessa forma:
Isso somente se entre e a função for contínua, isso é sem buracos, saltos ou quinas.
Lembre-se da tabela de primitivas:
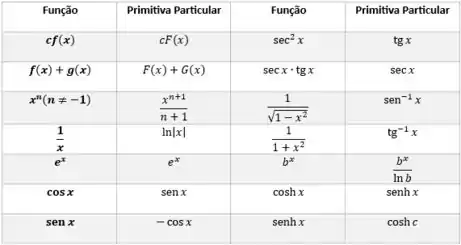
E aqui usaremos a da constante e a da .
Outra propriedade que vamos aplicar é que a integral de uma soma é a soma das integrais, assim:
Prooonto! Temos tudo em mãos para derrotar esse chefão!
Preparados?!
Passo 2
Primeiramente devemos achar a integral indefinida geral dessa função:
Separando essas integrais:
Integrando:
E não esqueça da constante! Aqui podemos colocar só um , para simbolizar as duas constantes, uma de cada integral.
Logo, também pelo Teorema fundamental do Cálculo, a integral definida é:
Nesse caso e
Sempre preste bastante atenção com os sinais!
E aí! o que achou? Responde Aí!
