Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 12

Calcule a integral dada, colocando-a em coordenadas polares.

∬ R 4 - x 2 - y 2   d A ,

onde R = x , y   x 2 + y 2 ≤ 4 ,   x ≥ 0 } .

Passo 1

Fala galera, beleza!!?

Precisamos calcular a seguinte integral em coordenadas polares:

∬ R 4 - x 2 - y 2   d A ,

onde R = x , y   x 2 + y 2 ≤ 4 ,   x ≥ 0 } .

Primeiro de tudo, lembra como é coordenadas polares? Vamos juntos revisar!

Para uma circunferência, cuja a expressão geral é:

x 2 + y 2 = r 2

Escrevemos em coordenadas polares assim:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Agora vamos avaliar nossa região R . Repare que temos a equação de um círculo cujo raio é 2 :

x 2 + y 2 ≤ 4

x 2 + y 2 ≤ 2 2

Nosso grande desafio agora é definir os intervalos de integração. O raio é mais fácil, já sabemos que vai de 0 até 2 .

Para o ângulo devemos prestar muito atenção!!! Ele quer somente para:

x ≥ 0

Isso impacta que nossa região é somente o primeiro e quarto quadrante.

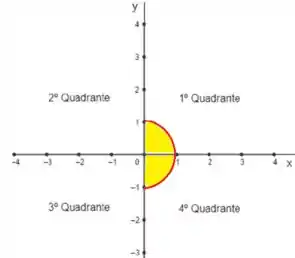
Logo temos que nossos intervalos de integração são:

0 ≤ r ≤ 2

- π / 2 ≤ θ ≤ π / 2

Viu como não é difícil, só tem que fazer com calma! Agora você vai montar a integral e achar seu valor!

Vamos nessa!

Passo 2

Nossa integral é:

∬ R 4 - x 2 - y 2   d A

Em coordenadas polares temos que: x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Como d A = d x d y , substituindo vamos ter:

∬ R 4 - ( r cos ⁡ θ ) 2 - ( r   s e n   θ ) 2   r d r d θ

Sabendo da relação trigonométrica:

cos 2 ⁡ x + s e n 2 x = 1

Simplificando temos:

∬ R 4 - r 2   r d r d θ

Passo 3

Lembra que nossa região de integração é:

R = x , y   x 2 + y 2 ≤ 4 ,   x ≥ 0 }

Perceba que temos um círculo de raio 2 comparando com a expressão geral do círculo:

x 2 + y 2 = r 2

Como a região de integração é dentro do círculo de raio 2 , devemos ter 0 ≤ r ≤ 2 .

Além disso, como estamos restritos a regiões com x ≥ 0 , ou seja, estamos no 1º e 4º quadrante apenas:

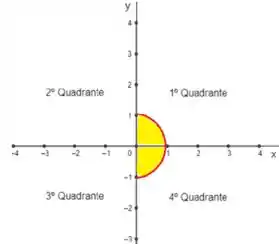
Logo, devemos ter a variação de ângulo igual a:

- π / 2 ≤ θ ≤ π / 2

Substituindo na integral, vamos ter:

∫ - π / 2 π / 2 ∫ 0 2 r   4 - r 2   d r   d θ

Passo 4

Agora devemos integrar. Como devemos começar integrando de dentro para fora, vamos começar integrando em d r .

∫ - π / 2 π / 2 ∫ 0 2 r   4 - r 2   d r   d θ

Aqui devemos fazer uma substituição do tipo:

u = 4 - r 2

d u d r = - 2 r   ∴ - d u 2 = r d r

Substituindo, temos:

∫ - π / 2 π / 2 ∫ 0 2   u   - d u 2   d θ

Integrando em d u e voltando para a variável r , temos que:

∫ - π / 2 π / 2 - 1 2 2 3 4 - r 2 3 2 0 2 d θ

Aplicando os limites de integração, temos:

∫ - π / 2 π / 2 - 1 2 2 3 4 - 2 2 3 2 - 2 3 4 - 0 2 3 2 d θ

Resolvendo, vamos ter:

∫ - π / 2 π / 2 8 3 d θ

Integrando em d θ agora, vamos ter:

8 3 ( θ ) - π 2 π 2

Aplicando os limites de integração, temos:

8 3 π 2 - - π 2  

Logo nossa resposta é:

∬ R 4 - x 2 - y 2   d A = ∫ - π / 2 π / 2 ∫ 0 2 r   4 - r 2   d r   d θ = 8 π 3

Resposta

8 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use coordenadas polares para determinar o volume do sólido dado.Limitado pelo paraboloide z = 6 - x 2 - y 2 e z = 2 x 2 + 2 y 2 .
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 2 ∫ 0 2 x - x 2x 2 + y 2 d y d x
Um irrigador agrícola distribui água em um padrão circular com raio de 100 pés. Ele fornece água a uma profundidade de e - r pés por hora a uma distância de r pés do irrigador.Se 0R ≤ 100 , qual é a q
Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .
Use coordenadas polares para determinar o volume do sólido dado.Acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2 + z 2 = 1 .