Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 26

Use coordenadas polares para determinar o volume do sólido dado.

Limitado pelo paraboloide z = 6 - x 2 - y 2 e z = 2 x 2 + 2 y 2 .

Passo 1

E aiiii meus queridooos, tudo na paz? Partiu resolver mais uma!

Bom, precisamos determinar o volume de um sólido em coordenadas polares. Sendo que esse solido, está limitado pelos paraboloides z = 6 - x 2 - y 2 e z = 2 x 2 + 2 y 2 .

Tá, mas e agora! Como resolvo isso?

Vamos lembrar que o volume pode ser representado pela seguinte integral:

V = ∬ D z d A

Importante lembrar que temos duas regiões escritas em função de z , logo ao montar a integral ter cuidado de substituir o z pelo: sólido que está a cima menos o sólido que está abaixo.

Também precisamos definir os limites da região D para montar a integral iterada, que vai ficar com essa cara:

V = ∫ a b ∫ c d ( z p a r a b o l o i d e a c i m a - z p a r a b o l o i d e a b a i x o ) d A

Nessa parte é importante fazer um esboço, para saber qual paraboloide está acima.

Agora vamos escrever tudo em função de coordenadas polares:

x = r cos ⁡ θ ;                 y = r sen ⁡ θ

d A = r d r d θ

Sabemos que 0 ≤ θ ≤ 2 π , já para o intervalo do raio você vai ter que substituir a equação do cone dentro da equação da esfera tudo em coordenadas polares.

Com esse bizu monstro, ficou tranquilo ein!! Vamos colocar mão na massa então!

Passo 2

Vamos escrever em coordenadas polares ambos os paraboloides, para determinar qual o raio.

Temos que uma das equações do paraboloide é dada por:

z = 6 - x 2 - y 2

Em coordenadas polares, temos que:

x = r cos ⁡ θ

y = r sen ⁡ θ

Substituindo temos que:

z = 6 - ( r c o s   θ ) 2 - ( r s e n   θ ) 2

z = 6 - r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ

z = 6 - r 2 ( cos 2 ⁡ θ + sen 2 ⁡ θ )

Utilizamos da relação trigonométrica para simplificar: cos 2 ⁡ θ + sen 2 ⁡ θ = 1 . Assim, temos:

z = 6 - r 2

Temos que a outra equação do paraboloide é dada por:

z = 2 x 2 + 2 y 2

Em coordenadas polares, temos que:

x = r cos ⁡ θ

y = r sen ⁡ θ

Substituindo temos que:

z = 2 r c o s   θ 2 + 2 ( r s e n   θ ) 2

z = 2 r 2 cos 2 ⁡ θ + 2 r 2 sen 2 ⁡ θ

z = 2 r 2 ( cos 2 ⁡ θ + sen 2 ⁡ θ )

Utilizamos da relação trigonométrica para simplificar: cos 2 ⁡ θ + sen 2 ⁡ θ = 1 . Assim, temos:

z = 2 r 2

Agora, devemos igualar as duas equações encontradas em coordenadas polares:

z = 6 - r 2

z = 2 r 2

Igualando, e isolando o r :

6 - r 2 = 2 r 2

6 = 2 r 2 + r 2

6 = 3 r 2

r 2 = 2

r = 2

Logo nosso intervalo de r é:

0 ≤ r ≤ 2

Passo 3

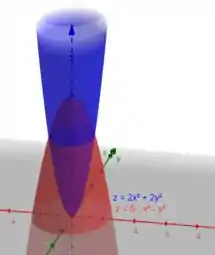
Antes de montar nossa integral, precisamos fazer um esboço dos paraboloides para saber qual deles esta abaixo e acima da região que queremos calcular o volume.

Temos os dois paraboloides:

z = 6 - x 2 - y 2

z = 2 x 2 + 2 y 2

Veja o esboço:

Analise com calma e repare que a região que desejamos, está acima de z = 2 x 2 + 2 y 2 e abaixo de z = 6 - x 2 - y 2

Passo 4

Sabendo disso, agora podemos montar nossa integral iterada.

V = ∫ a b ∫ c d ( z p a r a b o l o i d e a c i m a - z p a r a b o l o i d e a b a i x o ) d A

Onde, os paraboloides são:

z p a r a b o l o i d e a c i m a = 6 - x 2 - y 2

z p a r a b o l o i d e a b a i x o = 2 x 2 + 2 y 2

Em coordenadas polares:

z p a r a b o l o i d e a b a i x o = 2 r 2

Onde D será a região delimitada por:

0 ≤ r ≤ 2 ,     0 ≤ θ ≤ 2 π

d A = r d r d θ

Vamos substituir na integral. Nossa integral fica:

V = ∫ 0 2 π ∫ 0 2 6 - r 2 - 2 r 2 r d r d θ

V = ∫ 0 2 π ∫ 0 2 6 - 3 r 2 r d r d θ

V = ∫ 0 2 π ∫ 0 2 6 r - 3 r 3 d r d θ

Passo 5

Agora, vamos começar resolvendo a integral de dentro. Temos:

V = ∫ 0 2 π ∫ 0 2 6 r - 3 r 3 d r d θ

Integrando,

V = ∫ 0 2 π 6 r 2 2 - 3 r 4 4 0 2 d θ

Aplicando os limites de integração:

V = ∫ 0 2 π 6 2 2 2 - 3 4 2 4 d θ

V = ∫ 0 2 π 12 2 - 12 4 d θ

Logo, ficamos com:

V = ∫ 0 2 π 3 d θ

Agora, restou uma integral simples em d θ .

Integrando, temos:

V = ∫ 0 2 π 3 d θ = 3 θ 0 2 π

Aplicando os limites de integração:

V = 3 2 π

Portanto o volume vale:

V = 6 π

Resposta

V = 6 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∬ R ( x 2 + y 2 ) d x d y , sendo R é dada por:b) Círculo centrado em ( a ,0 ) de raio a .
Calcular ∬ R d x d y , onde R é delimitada pela elipse 4 x - 3 2 + y - 2 2 = 4 . Interpretar geometricamente.
Calcular ∬_R^() cos (x^2 + 9 y^2) d x d y , sendo R dada por x^2 + 9 y^2 = 1 e x = 0 .
Calcular ∬ R x 2 + y 2 d x d y , sendo R a região interna à circunferência x 2 + y 2 = 4 y e externa à circunferência x 2 + y 2 = 2 y .
Calcular ∬ R ( x 2 + y 2 ) d x d y , sendo R é dada por:c) Círculo centrado em ( 0 ,a ) de raio a .