Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 11

Calcule a integral dada, colocando-a em coordenadas polares.

∫ ∫ R cos ⁡ x 2 + y 2   d A ,

onde R é a região acima do eixo x e dentro da circunferência x 2 + y 2 = 9 .

Passo 1

Vamos lá pessoal, tudo certo? O exercício quer que calculemos em coordenadas polares a seguinte integral:

∫ ∫ R cos ⁡ x 2 + y 2   d A

Sobre uma região R que é parte superior de um semicírculo. O primiro passo, é identificar exatamente qual a região de integração e os limites de integração. Após isso, iremos utilizar as relações de transformação para fazer as alterações necessárias para integral polar.

Veja as relações que iremos utilizar são:

x = r cos ⁡ θ           e         y = r   s e n   θ

Além disso,

x 2 + y 2 = r 2

Ou seja:

x 2 + y 2 = 9

Significa que   r = 3 .

O primeiro passo aqui é desenhar a região de integração:

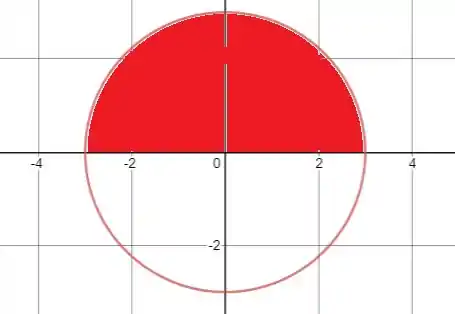
Passo 2

Vamos então identificar os limites de integração, como estamos considerando apenas a região acima do eixo x , o ângulo polar varia entre

0 ≤ θ ≤ π

Já o raio r varia entre

0 ≤ r ≤ 3

Após isso é só integrar. Vamos começar a execução?

Lembrando que

x = r cos ⁡ θ           e         y = r   s e n   θ

Assim,

x 2 + y 2 = r 2

Passando para coordenadas polares, temos que

∫ ∫ R cos ⁡ x 2 + y 2   d A = ∫ 0 π ∫ 0 3 cos ⁡ r 2 ⋅ r   d r   d θ

Passo 3

Nunca esqueça do jacobiano r quando passamos para coordenadas polares! Como o integrando não depende de θ , podemos fazer a integral nessa variável de cara:

∫ ∫ R cos ⁡ x 2 + y 2   d A = π   ∫ 0 3 cos ⁡ r 2   r   d r

Chamando u = r 2 , temos que

d u = 2 r   d r ⇒ r   d r = d u 2

Além disso, quando r = 0 , temos u = 0 . Já para r = 3 , achamos u = 9 . Assim,

∫ ∫ R cos ⁡ x 2 + y 2   d A = π 2 ∫ 0 9 cos ⁡ u   d u

Fazendo a integral

∫ ∫ R cos ⁡ x 2 + y 2   d A = π 2 s e n   u 0 9 = π 2 s e n   9 - s e n   0

Logo,

∫ ∫ R cos ⁡ x 2 + y 2   d A = π 2   s e n   9

Resposta

π 2   s e n   9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .6-
Calcule a integral iterada, convertendo-a antes para coordenadas polares.30- ∫ - a a ∫ 0 a 2 - y 2 x 2 + y 2 3 2d xd y
33- Uma piscina circular tem 40p é s é de diâmetro. Sua profundidade é constante na direção leste-oeste e aumenta linearmente de 2p é s é no término sul para 7p é s é no término norte. Determine o vol
Um aspersor distribuí água em um círculo de raio de 100 pés. Ele fornece água até uma profundidade e - r pés por hora em uma distância de r pés do aspersor.Qual a quantidade total de água fornecida po
Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .