Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 1

Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Ele fornece uma região R , e precisamos calcular a integral dupla iterada nessa região. Sabendo disso, devemos escolher coordenadas polares ou retangulares. A integral é:

∬ R f x , y d A

Como resolvemos essa? Deu um branco.

Primeiro vamos lembrar de integral iterada, que isso?

É uma integral com intervalos de integração, e ela tem essa cara:

∫ a b ∫ c d f x , y d A

Agora, observe com calma a imagem que ele forneceu, repare que ela apresenta dois círculos, um com raio 2 e outro com raio 5 . Nossa região   R está entre esses dois círculos:

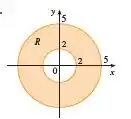
Agora vamos ter que lembrar da equação de um círculo, que tem essa cara:

x 2 + y 2 = r 2

Para círculo, torna-se mais cômodo utilizar coordenadas polares. E assim, temos que:

x = r cos ⁡ θ ;                 y = r sen ⁡ θ

d A = r d r d θ

Sabendo disso, definimos os intervalos da integral iterada. Observe nossa região R (em amarelo), temos r indo de 2 a 5 . E θ de 0 a 2 π , logo:

2 ≤ r ≤ 5 ,   0 ≤ θ ≤ 2 π

Agora é só montarmos a integral dupla iterada e gabaritar!! Bora lá juntos!

Passo 2

Bom... Queremos representar a integral dupla ∬ R f x , y d A como uma integral iterada.

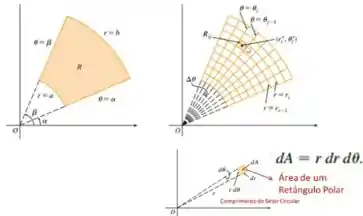
Primeiro vamos lembrar como representar o elemento d A em coordenadas polares, observe a imagem abaixo.

Pegamos um pequeno elemento infinitesimal de área d A , e observamos que a área dele pode ser aproximada pelo r (raio) vezes o comprimento de curva d r d θ .

Passo 3

Sabendo que:

d A = r d r d θ

E as coordenadas x e y são:

x = r cos ⁡ θ

y = r sen ⁡ θ

E os intervalos de integração para r e θ são:

2 ≤ r ≤ 5

0 ≤ θ ≤ 2 π

Agora podemos montar nossa integral dupla iterada:

∫ a b ∫ c d f x , y d A

Logo, temos que:

∬ R f x , y d A = ∫ 0 2 π ∫ 2 5 f r cos ⁡ θ ,   r sen ⁡ θ r d r d θ

Resposta

∬ R f x , y d A = ∫ 0 2 π ∫ 2 5 f r cos ⁡ θ ,   r sen ⁡ θ r d r d θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da região D de plano x y definida por D = x , y ∈ R 2 x 2 + y - 2 2 ≤ 4ex 2 + y 24 .
Calcule, usando mudança polar, as seguintes integrais: ∫ ∫ D x 2 + y 2 d x d y , onde D é a região no primeiro quadrante do pano x y limitada por x 2 + y 2 = 1 , x 2 + y 2 = 4 , y = x e y = 3 3 x .
Calcule, usando mudança polar, as seguintes integrais: ∫ ∫ D x 2 yd x d y , onde D = { ( x , y ) ∈ R 2 | x - 1 2 + y 2 ≤ 1 }
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .