Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 12

Calcule a integral dada, colocando-a em coordenadas polares.

12.

∬ D cos ⁡ x 2 + y 2 d A

Onde D é o disco com centro na origem e raio 2.

Passo 1

Fala, galera!

A questão nos pede parar mudar a função de integração de coordenadas cartesianas para coordenadas polares e depois calcular. Moleza, né?

Vamos lembrar algumas fórmulas que podemos usar para polar:

y = r s e n θ x = r c o s θ x 2 + y 2 = r 2 d A = r   d r   d θ

Assim, vamos transformar:

∬ D cos ⁡ x 2 + y 2 d A

∬ D cos ⁡ r 2 d A

∬ D r cos ⁡ ( r ) d r d θ

Agora precisamos escrever a nossa região em coordenadas polares.

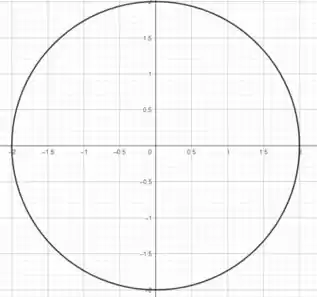
O valor do raio r varia de 0 até o círculo de raio 2, logo

0 ≤ r ≤ 2

Já o valor de θ varia de 0 até 2 π , pois a nossa região D descreve todo o círculo de raio 2.

0 ≤ θ ≤ 2 π

Passo 2

Agora que descrevemos a região em coordenadas polares, podemos colocar os limites de integração na nossa integral. Portanto,

∫ 0 2 π ∫ 0 2 r cos ⁡ ( r ) d r   d θ

Resolvemos primeiro a integral de dentro.

∫ 0 2 r cos ⁡ ( r ) d r

Como temos dentro da integral uma função trigonométrica e um polinômio, usaremos a técnica de integração por partes. Para isto, basta lembrar da fórmula:

∫ u d v = u v - ∫ v d u

Seja u = r , então d u = d r .

Também seja d v = cos ⁡ r d r , então v = sen ⁡ r .

Logo,

∫ r c o s r d r = r sen ⁡ r - ∫ s e n r d r

= r sen ⁡ r + cos ⁡ r 0 2

= 2 sen ⁡ 2 + cos ⁡ 2 - 1

Passo 3

Resolvendo, agora, a integral de fora:

∫ 0 2 π 2 sen ⁡ 2 + cos ⁡ 2 - 1 d θ

2 sen ⁡ 2 + cos ⁡ 2 - 1 ∫ 0 2 π d θ

2 sen ⁡ 2 + cos ⁡ 2 - 1 ⋅ θ 0 2 π

2 sen ⁡ 2 + cos ⁡ 2 - 1 ⋅ 2 π

Resposta

2 sen ⁡ 2 + cos ⁡ 2 - 1 ⋅ 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Calcule a integral dada, colocando-a em coordenadas polares. ∫ ∫ R x + yd A , onde R é a região que está a esquerda do eixo y e entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .
Calcule a integral dada, colocando-a em coordenadas polares.13. ∬ R a r c t gy xd A Onde R = x , y1 ≤ x 2 + y 2 ≤ 4 ,0 ≤ y ≤ x } .
Utilize a integral dupla para determinar a área da região.Um laço de rosácea r = cos ⁡ 3 θ .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ De - x 2 - y 2d A , onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .