Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 10
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
10.
Passo 1
Fala, gente bonita!
A questão manda a gente calcular essa integral dupla, dando pra gente os limites de integração da região, moleza né? Mas antes quer que a gente identifique-a com o volume de um sólido.
Estamos trabalhando com volume, uma região com três dimensões.
Nós podemos interpretar essa integral assim, ó:
Se nosso sólido tiver , a altura dele será , beleza?
Temos outros limites de integração dados no enunciado que definem a região, veja:
Como todas as informações nos dizem que as regiões são positivas, podemos representar o sólido um prisma triangular de base quadrada. Assim, temos um esboço:
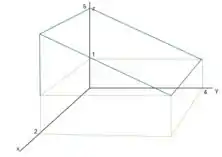
Passo 2
Para calcular o volume do sólido, podemos fazer a integral dessa região ou fazer de um jeito bem mais rápido. Olha só!
Temos que considerar a altura quando
Não podemos passar disso, já que .
Por isso vamos calcular nosso primeiro volume, do cubo (no desenho representado em verde)
E o volume do prisma (representado em azul):
Na altura total , precisamos subtrair já que nosso prisma começa a partir dele, então:
Assim, somando os volumes, teremos que