Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 11
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos lá!
Vamos visualizar o sólido representado pela integral dupla dada. Este sólido está contido no retângulo no plano e se estende verticalmente até , sendo cortado pelo plano .
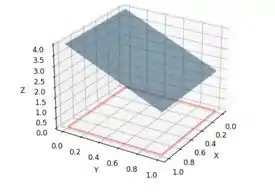
Para entender melhor o sólido, observe que quando , temos o plano , formando uma parte retangular do sólido. De até, o sólido assume uma forma triangular, com base e altura .
Passo 2
O volume total do sólido é composto pela parte retangular e pela parte triangular :
O valor da integral dupla então é 3.
Resposta
Exercícios de Livros Relacionados
Calcule a integral iterada.int_0^2 int_0^(pi) r s e n^2 theta d theta d r
Calcule a integral iterada.int_0^1 int_0^1 sqrt(s + t) d s d t
Calcule a integral iterada.int_0^1 int_0^1 x y . sqrt(x^2 + y^2) d y d x
Calcule a integral iterada.int_0^1 int_0^1 (u - v)^5 d u d v
Encontre o volume do sólido delimitado pela superfície z = x sec 2 y e pelos planos z = 0, x = 0, x = 2, y = 0 e y = π 4 .