Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 14
Expresse como a região do tipo e também como uma região do tipo . Em seguida, calcule a integral dupla de duas maneiras.
Passo 1
Fala, meus amigos! Tudo joia?
A questão pede para expressarmos a região :
Como uma região do tipo I e como uma região do tipo II. Recapitulando sobre as regiões:
As regiões planas das integrais duplas são os domínios de integração sobre o qual a integral é calculada. Esta região é definida pelos limites de integração para as variáveis envolvidas.
- Regiões do Tipo I: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
- Regiões do Tipo II: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar abaixo da outra no eixo , assim a região fica confinada entre e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar antes da outra no eixo , assim a região fica confinada entre e .
Por fim, vamos precisar calcular:
De dois jeitos, ou seja, considerando como uma região do tipo I e novamente, considerando como uma região do tipo II.
Bora lá?
Passo 2
Primeiro vamos entender como é nossa região . Como é limitado pelas retas e , vamos plotar estas retas para ver como fica a região :
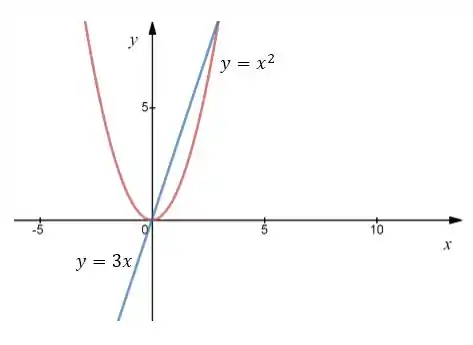
Nosso objetivo é expressar como uma região do tipo e também do tipo e em seguida encontrar a integral dupla das duas maneiras.
Passo 3
Podemos definir esta região como do tipo , quando:
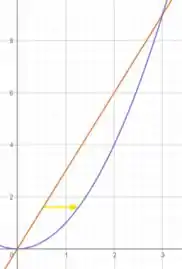
E já podemos resolver a integral para esse caso. Como nosso limite de integração de tem um termo em função de , vamos colocar a integral de “por dentro”, assim ela vai ser resolvida primeiro e vai facilitar bastante nosso cálculo.
Temos então que:
Vamos resolver a integral de dentro:
Logo:
Resolvendo, temos:
Portanto:
Passo 4
Agora vamos definir como uma região do tipo . Temos:
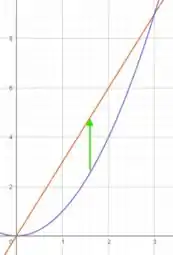
E já podemos resolver a integral para esse caso. Como nosso limite de integração de tem um termo em função de , vamos colocar a integral de “por dentro”, assim ela vai ser resolvida primeiro e vai facilitar bastante nosso cálculo.
Temos então que:
Vamos resolver a integral de dentro:
Logo:
Resolvendo, temos:
Portanto: