Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.2 - Ex. 29
Encontre o volume do sólido delimitado pela superfície e pelos planos e .
Passo 1
E aiiiiiiiiii galerinha, tudo bem? Vamos começar!!
Nosso objetivo é encontrar o volume do sólido delimitado pela superfície e pelos planos e .
Vish, agora lascou? Calma, vamos pensar juntos em uma estratégia de resolução!!
Lembre-se da fórmula geral de volume, que é a seguinte:
Onde, é a função que delimita a região, e é nossa região de integração, que nesse caso vai ser delimitado pelos planos.
Observe a variação de e , temos um retângulo que é formado pelos planos. Assim, temos que:
Já temos os intervalos da nossa região .
Agora vamos olhar para . Observe que ele deu no enunciado que varia entre uma função e o plano . Sabendo disso, podemos definir nossa altura .
Que vai ser:
Coisa linda ein!!!! Agora podemos montar nossa integral e colocar mão na massa. Vamos nessa!
Passo 2
Pessoal, vamos montar nossa integral de volume primeiro.
Vamos relembrar. Sabemos que:
Logo, obtemos a seguinte integral:
Agora precisamos começar a integrar. E lembre-se, sempre começamos a integrar de dentro para fora, ou seja, começamos por .
Passo 3
Vamos começar a integrar em .
Integrando, vamos ter:
Aplicando os limites de integração:
Simplificando:
Passo 4
Agora, é só resolver a integral simples que restou.
A integral da secante ao quadrado, é uma integral bastante conhecida. Sabemos que:
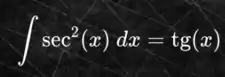
Tendo essa informação em mãos, podemos dizer que:
Aplicando os limites de integração, vamos ter: