Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 4
Calcule a integral fazendo a substituição dada.
Passo 1
Opa! Blz?
Bora resolver essa integral aqui:
Pra isso vamos usar a Regra da Substituição e o enunciado já diz pra a gente qual substituição fazer:
Mas o que é a integração por substituição?
Lembra que a integral é a operação contraria da primitiva? Então temos que ela deve ser realmente o inverso da regra da cadeia. De acordo com a regra da cadeia para a derivada temos:
Na integração por substituição, pegamos uma expressão da forma e encontramos sua primitiva.
A integração por substituição nos ajuda a simplificar uma expressão confusa, transformando a função "interna" na variável. Então temos que encontrar o resultado dessa integral:
Para simplificar essa integral, colocamos uma nova variável tal que . Isso significa que .
Substituindo essas expressões na integral, obtemos:
A integral agora é muito mais simples de resolver, pois é uma função direta de . Após integrar em relação a , obtemos .
Finalmente, substituímos de volta por para obter a resposta na variável original .
Agora que já sabemos o que precisamos fazer, mãos a massa!
Passo 2
Agora vamos achar a derivada de :
Assim conseguimos isolar o :
Vamos agora fazer a substituição:
Então temos que resolver a seguinte integral:
Agora fica simples de resolver, vamos lá.
Agora é fácil achar as primitivas da função, usando duas expressões da Tabela de Integrais Indefinidas (primitivas):
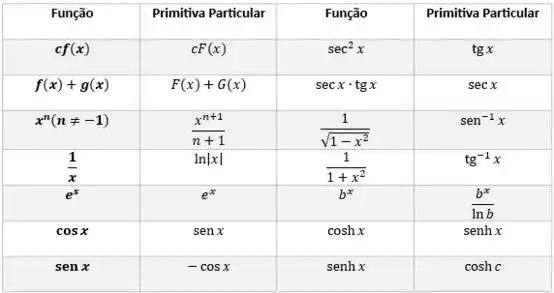
Agora é só aplicar, vamos colocar a constante multiplicativas para fora:
E agora aplicando a regra da primitiva para potencias:
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo, no caso aqui foi :
Prontinho!