Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 43
Calcule a integral indefinada. Ilustre e verifique se sua resposta é razoável, usando o gráfico da função e de sua primitiva (tome .
Passo 1
Para este caso vamos aplicar a técnica de integração por partes. Para isso precisamos dividir o argumento da integral em duas funções e respectivamente. Feito isso, aplicamos a fórmula para a integração por partes que é dada por :
Ou de forma mais visível, fazemos:
Primeiro então, devemos definir quem vão ser nossas funções. É aconselhável escolher a função mais fácil de derivar para ser . Assim:
Derivando e integrando , temos:
Observe que aplicamos a integração por substituição na integral com a exponencial, lembre-se que esse método consiste em fazer uma troca de uma parte de uma função por uma variável simples e que resulte em um conveniente que irá possibilitar a integração, geralmente esse resultado é parte de outra função contida no integrando. Após integrar, você deve substituir a variável simples pela função que você a usou para substituir. Logo:
Passo 2
Aplicando as funções e suas derivadas na fórmula citada no passo anterior, temos:
Passo 3
Tomando , e esboçando o gráfico da função e de sua primitiva temos:
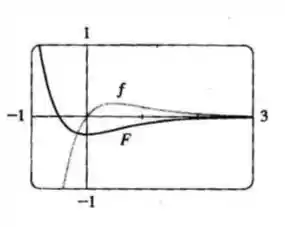
Verificamos que a resposta é sim razoável pois tem um mínimo onde muda de negativo para positivo. Além disso, aumenta onde é positivo e diminui onde é negativo.
Resposta
Ei, a resposta está no passo a passo :)