Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.2 - Ex. 53

Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável colocando em um gráfico um integrando e sua primitiva (tome c = 0 ).

∫ sin ⁡ 3 x sin ⁡ 6 x d x

Passo 1

Calma jovem, vamos calcular essa integral de um jeito que você vai entender, vamos lá? Precisamos lembrar da seguinte propriedade trigonométrica:

sin ⁡ A sin ⁡ B = 1 2 cos ⁡ A - B - cos ⁡ A + B

Substituindo

∫ sin ⁡ 3 x sin ⁡ 6 x d x = 1 2 ∫ cos ⁡ 3 x - 6 x - cos ⁡ 3 x + 6 x d x = 1 2 ∫ cos ⁡ 3 x - cos ⁡ 9 x d x = 1 2 1 3 sin ⁡ 3 x - 1 9 sin ⁡ 9 x + c = 1 6 sin ⁡ 3 x - 1 18 sin ⁡ 9 x + c

Passo 2

Esboçando os gráficos, ficamos com ( f → p r e t o ,     F → c i n z a )

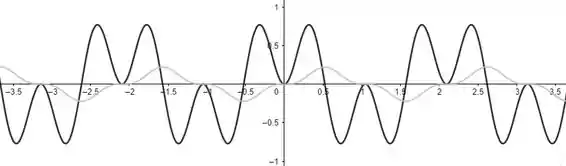
Observe que f ( x ) = 0 sempre que F tem uma tangente horizontal.

Resposta

∫ sin ⁡ 3 x sin ⁡ 6 x d x = 1 6 sin ⁡ 3 x - 1 18 sin ⁡ 9 x + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 31 a 36, calcule a integral definida. 34 )∫ 0 π 3 t g 3 x sec ⁡ x . d x
Nos Exercícios de 1 a 30, calcule a integral indefinida. 28 )∫ s e n 2 ( π x ) cos 6⁡ ( π x ) . d x
Nos Exercícios de 31 a 36, calcule a integral definida. 36 )∫ π 6 π 4 c o t g ³ w . d w ³
Nos Exercícios de 31 a 36, calcule a integral definida. 31 )∫ π 16 π 12 t g ³4 x . d x ³
Nos Exercícios de 31 a 36, calcule a integral definida. 33 )∫ - π 4 π 4 sec 6 ⁡ ( x ) . d x