Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.5 - Ex. 48
Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável fazendo o gráfico da função e de sua primitiva (tome ).
Passo 1
Oie!
Temos a seguinte integral indefinida:
Além de resolver ela, precisamos trazer seu gráfico e de sua primitiva e compara-los!
Mas como vamos resolver essa integral?
Vamos usar a regra da substituição, onde vamos chamar uma parte da função de (geramente a parte mais complicadinha da função), vamos calcular como a derivada de em relação a , geralmente essa derivada é idêntica ao resto da nossa função (mas em alguns casos precisamos dar uma manipuladinha).
Para essa derivada vamos usar a regra da potência:
Aí resolvemos a integral em função de , e para facilitar nossa vida vamos usar a tabela de integrais:
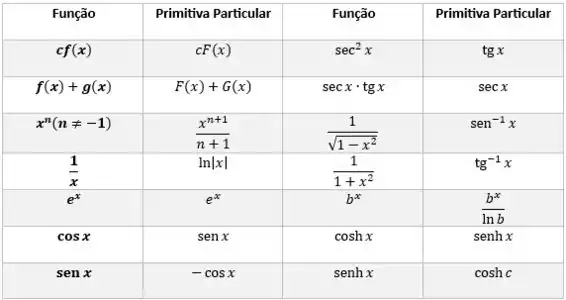
Depois voltamos para seu valor original!
Por fim, plotamos o gráfico usando algum software!
Portinho, mão na massa!
Passo 2
Vamos tentar a substituição , então vamos calcular :
Aqui precisamos olhar para a nossa função original:
Repare que a parte que colocamos entre os parentes é bem parecida com a nossa integral, então para ficar idêntica vamos passar o 2 para o outro lado:
Desta forma, a integral, após a substituição, pode ser escrita como
Lembra que podemos colocar uma constante multiplicativa para fora da integral?
Agora olhando a tabela:
Voltando para a variável :
Passo 3
Tomando , que foi passado no enunciado, em vermelho fazemos o gráfico da função e em azul o de sua primitiva/integral:
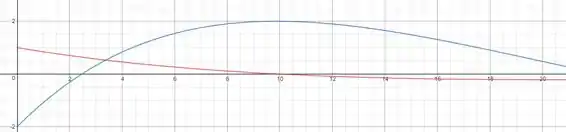
Note que o sinal da curva vermelha comanda o crescimento da curva azul: esse é exatamente o comportamento que a derivada de uma função deve ter. Mas pera aí, uma função é a derivada de sua primitiva, então é exatamente isso que devemos esperar!