Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.5 - Ex. 49
Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável fazendo o gráfico da função e de sua primitiva (tome ).
Passo 1
Pessoal nessa questão devemos calcular a seguinte integral:
E depois devemos tomar o gráfico da função e da primitiva, usando e verificar se a resposta é razoável.
Para resolver a integral, a técnica da substituição parece ser uma boa opção...
Sabemos disso, pois temos um fator que possui e a sua derivada que possui aparece no resto da integral. Isso é importante para que após a substituição tudo esteja escrito em termos da nova variável .
Para a técnica da substituição devemos pegar parte do termo que está sendo integrado e chama-lo de .
Então, devemos encontrar derivando em termos de .
E portanto teremos que:
E dessa forma, substituímos a diferencial de da integral.
Por fim, basta resolver a integral e desfazer a substituição.
Passo 2
Assim, fazendo que:
Teremos que:
Dessa forma, substituindo teremos:
Resolvendo usando a regra da potência, temos:
Voltando para a variável :
Passo 3
Tomando , em vermelho fazemos o gráfico da função e em azul o de sua primitiva:
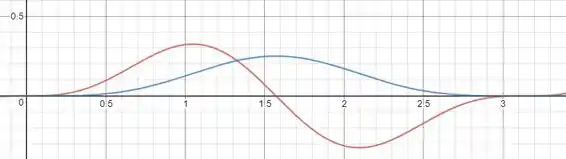
Observe que quando a curva em vermelho se anula, sua primitiva em azul tem tangente horizontal (derivada zero). Além disso, o sinal da curva vermelha comanda o crescimento da curva azul. Isso significa que nossa resposta para a primitiva da função é bastante razoável.