Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 46

Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável usando o gráfico da função e de sua primitiva ( C = 0 ) .

∫ x ² se n ⁡ 2 x d x

Passo 1

Primeiro a gente diz que

u = x 2 ,   d v = se n ⁡ 2 x d x → d u = 2 x   d x ,   v = - 1 2 cos ⁡ 2 x

Passo 2

Assim, temos que

I = ∫ x ² se n ⁡ 2 x d x = - 1 2 x 2 cos ⁡ 2 x + ∫ x cos ⁡ 2 x   d x

O próximo passo é fazer outra substituição (não desiste que vai dar certo!):

U = x ,   d V = cos ⁡ 2 x d x → d U = d x ,   V = 1 2 se n ⁡ 2 x

Assim,

∫ x cos ⁡ 2 x   d x = 1 2 x se n ⁡ 2 x - ∫ 1 2 se n ⁡ 2 x   d x = 1 2 x se n ⁡ 2 x + 1 4 cos ⁡ 2 x + C

Agora pra finalmente concluir:

I = - 1 2 x 2 cos ⁡ 2 x + 1 2 x se n ⁡ 2 x + 1 4 cos ⁡ 2 x + C

Passo 3

Estimando um gráfico:

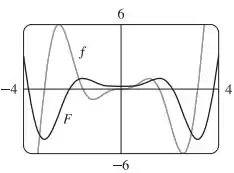
Nós conseguimos ver pelo gráfico que nosso cálculo foi razoável, já que F aumenta onde f é positiva e decresce onde f é negativa.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. 14 .∫ x cosh ⁡ a xd x
Primeiro faça uma substituição e depois use a integração por partes para avaliar a integral. 37 .∫ e xd x
Calcule a integral. 25 .∫ 0 2 y sinh ⁡ yd y
Calcule a integral. 29 .∫ 0 π x sin ⁡ x cos ⁡ xd x
Calcule a integral. 27 . ∫ 1 5 ln ⁡ R R 2d R