Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 24
Calcule a integral indefinida.
Passo 1
Eaee, belezinha?? Bom... queremos calcular a seguinte integral indefinida:
Bem, aqui vamos usar a Regra da Substituição!!
Mas o que é a integração por substituição?
Lembra que a integral é a operação contraria da primitiva? Então temos que ela deve ser realmente o inverso da regra da cadeia.
Na integração por substituição, pegamos uma expressão da forma e encontramos sua primitiva.
Então temos que encontrar o resultado dessa integral:
Para simplificar essa integral, colocamos uma nova variável tal que . Isso significa que .
Substituindo essas expressões na integral, obtemos:
Aí resolvemos a integral em relação a , obtemos .
Finalmente, substituímos de volta por para obter a resposta na variável original .
Vamos fazer uma mudança de variável para encontrar o valor dessa integral, vemos que temos multiplicando , ( também pode ser escrito como ) podemos então usar a mudança de variável:
Agora bora aplicar!! 😉
Passo 2
Vamos agora achar a derivada de :
Agora vamos comparar com nossa integral original:
Reescrevendo:
Repara que precisamos ter o que está entre colchetes, para isso precisamos passa 0 para o outro lado:
Vamos podemos fazer a substituição:
Agora fica simples de resolver, vamos lá!!
Passo 3
Agora é fácil achar as primitivas da função, usando duas expressões da Tabela de Integrais Indefinidas:
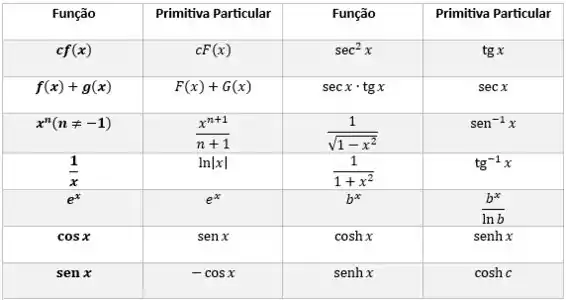
Agora é só aplicar:
Primeiro vamos colocar a constante multiplicativa para fora:
Agora aplicando a integral do seno:
Passo 4
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo, no caso aqui foi :
Temos enfim: