Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 38

Calcule a integral, interpretando-a em termos das áreas.

Passo 1

Fala aí, tudo certinho com você?

Bom, essa questão pede pra gente calcular a integral abaixo, interpretando-a em termos das áreas.

Sendo assim, vamos olhar pra a função que está sendo integrada e desenhar seu gráfico. Isso vai nos ajudar a entender essa integral como sendo um cálculo de área.

Vem comigo.

Passo 2

Desenhando o gráfico dessa função temos o seguinte:

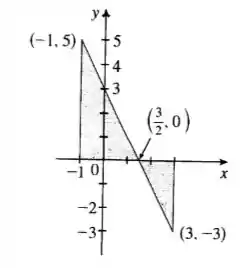
Observe que temos dois triângulos na imagem.

Assim a integral pode ser calculada como sendo a área dos dois triângulos. Mas observe, que há um que está abaixo do eixo , sendo assim sua área será contabilizada como sendo um valor negativo.

Passo 3

Essa integral pode ser interpretada como a área do triângulo sobre o eixo menos a área do triângulo abaixo do eixo , então:

Lembrando que a área do triângulo é calculada fazendo:

Assim, a integral se torna:

E prontinho.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a área da região limitada pela curva: y = 9 9 - x 2 pelos eixos coordenados e pela reta x = 2 2 .

Calcule a área da região situada no 1 ° quadrante, limitada acima pela curva x 4 - y 4 = 2 x y (coordenadas cartesianas) e abaixo por ρ 2 = 2 sen ⁡ 2 θ (coordenadas polares), com ρ ≥ 0 .

Calcule a área do conjunto de todos os pontos θ , ρ tais que θ 2 ≤ ρ ≤ θ (coordenadas polares).

Passe a curva dada para coordenadas polares e desenhe-a. x 2 + y 2 3 2 = y 2

Sejam F 1 e F 2 dois pontos distintos do plano e seja k a metade da distância de F 1 a F 2 . O lugar geométrico dos pontos P do plano tais que P F 1 - ⋅ P F 2 - = k 2 denomina-se lemniscata de focos F